题目内容
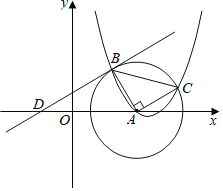
【题目】如图,已知![]() 的圆心为点
的圆心为点![]() ,抛物线
,抛物线![]() 过点
过点![]() ,与
,与![]() 交于
交于![]() 两点,连接
两点,连接![]() 、
、![]() ,且
,且![]() ,
,![]() 两点的纵坐标分别是2、1.
两点的纵坐标分别是2、1.
(1)请直接写出点![]() 的坐标,并求
的坐标,并求![]() 的值;
的值;
(2)直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() (与点
(与点![]() 不重合)在该直线上,且
不重合)在该直线上,且![]() ,请判断点
,请判断点![]() 是否在此抛物线上,并说明理由;
是否在此抛物线上,并说明理由;
(3)如果直线![]() 与
与![]() 相切,请直接写出满足此条件的直线解析式.
相切,请直接写出满足此条件的直线解析式.
【答案】(1)B(2,2),![]() ;(2)点
;(2)点![]() 在抛物线上,见解析;(3)满足条件的直线解析式为:
在抛物线上,见解析;(3)满足条件的直线解析式为:![]() 或
或![]() .
.
【解析】
(1)证明![]() ,即可求解;
,即可求解;
(2)点![]() 在直线
在直线![]() 上,则设
上,则设![]() 的坐标为
的坐标为![]() ,由
,由![]() ,即可求解;
,即可求解;
(3)分当切点在![]() 轴下方、切点在
轴下方、切点在![]() 轴上方两种情况,分别求解即可.
轴上方两种情况,分别求解即可.
解:(1)过点![]() 分别作
分别作![]() 轴的垂线交于点
轴的垂线交于点![]() ,
,
∵![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ,
,
故点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,
将点![]() 坐标代入抛物线
坐标代入抛物线![]() 并解得:
并解得:
![]() ,
,
故抛物线的表达式为:![]() ;
;
(2)将点![]() 坐标代入
坐标代入![]() 并解得:
并解得:![]() ,则点
,则点![]() ,
,
点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 、
、![]() 、
、![]() ,
,
则![]() ,
,
点![]() 在直线
在直线![]() 上,则设
上,则设![]() 的坐标为
的坐标为![]() ,
,
∵![]() ,则
,则![]() ,
,
解得:![]() 或6(舍去
或6(舍去![]() ),
),
故点![]() ,
,
把![]() 代入
代入![]() ,
,
故点![]() 在抛物线上;
在抛物线上;
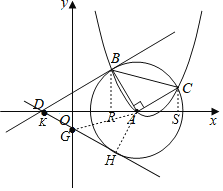
(3)①当切点在![]() 轴下方时,
轴下方时,
设直线![]() 与
与![]() 相切于点
相切于点![]() ,直线与
,直线与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,连接
,连接![]() ,
,
![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即:
,即:![]() ,
,
解得:![]() 或
或![]() (舍去
(舍去![]() ),
),
故点![]() ,
,
把点![]() 坐标代入
坐标代入![]() 并解得:
并解得:
直线的表达式为:![]() ;
;
②当切点在![]() 轴上方时,
轴上方时,
直线的表达式为:![]() ;
;
故满足条件的直线解析式为:![]() 或
或![]() .
.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如表:
售价 | 3元 | 4元 | 5元 | 6元 |
数目 | 14本 | 11本 | 10本 | 15本 |
下列说法正确的是( )
A. 该班级所售图书的总收入是226元
B. 在该班级所售图书价格组成的一组数据中,中位数是4
C. 在该班级所售图书价格组成的一纽数据中,众数是15
D. 在该班级所售图书价格组成的一组数据中,方差是2