题目内容
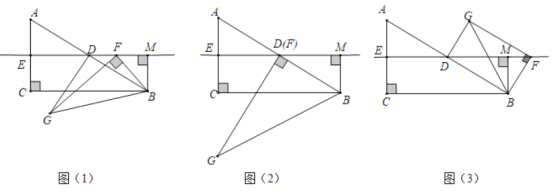
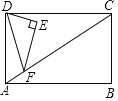
【题目】如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是________.
【答案】![]() .
.
【解析】
当F与A点重合时和F与C重合时,根据E的位置,可知E的运动路径是EE'的长;由已知条件可以推导出△DEE'是直角三角形,且∠DEE'=30°,在Rt△ADE'中,求出DE'=![]() 即可求解.
即可求解.
解:如图
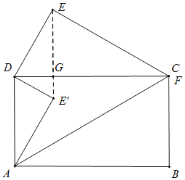
E的运动路径是EE'的长;
∵AB=4,∠DCA=30°,
∴BC=![]() ,
,
当F与A点重合时,
在Rt△ADE'中,AD=![]() ,∠DAE'=30°,∠ADE'=60°,
,∠DAE'=30°,∠ADE'=60°,
∴DE'=![]() ,∠CDE'=30°,
,∠CDE'=30°,
当F与C重合时,∠EDC=60°,
∴∠EDE'=90°,∠DEE'=30°,
在Rt△DEE'中,EE'=![]() ;
;
故答案为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目