题目内容
【题目】如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.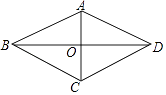
(1)求证:四边形ABCD是菱形;
(2)若CD=3,BD=2 ![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
【答案】
(1)证明:∵AB=AD,
∴∠ABD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠CBD,
∵AC⊥BD,AB=AD,
∴BO=DO,
在△AOD与△COB中, 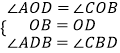 ,
,
∴△AOD≌△COB,
∴AO=OC,
∵AC⊥BD,
∴四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OD= ![]() BD=
BD= ![]() ,
,
∴OC= ![]() =2,
=2,
∵AC=4,
∴S菱形ABCD= ![]() ACBD=4
ACBD=4 ![]() .
.
【解析】(1)根据等腰三角形的性质得到∠ABD=∠ADB,根据角平分线的定义得到∠ABD=∠CBD,等量代换得到∠ADB=∠CBD,再根据全等三角形的性质得到AO=OC,由菱形的判别即可得到所求的结论结论;
(2)根据菱形的性质求得OD的值,再根据勾股定理得到OC的值,再菱形的面积公式求得所求答案.

练习册系列答案
相关题目