题目内容
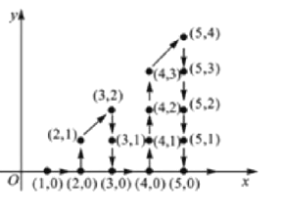
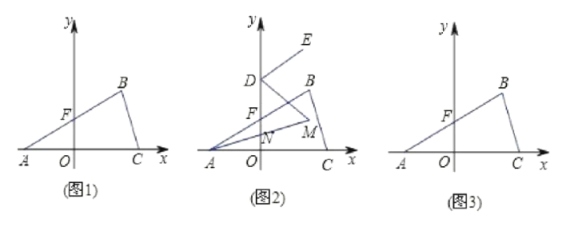
【题目】如(图1),在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,且满足
,且满足![]() ,线段
,线段![]() 交
交![]() 轴于
轴于![]() 点.
点.
(1)填空:![]() ,
,![]() ;
;
(2)点![]() 为
为![]() 轴正半轴上一点,若
轴正半轴上一点,若![]() ,
,![]() ,且
,且![]() 分别平分
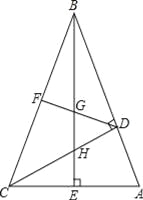
分别平分![]() ,如(图2),求
,如(图2),求![]() 的度数;
的度数;
(3)求点![]() 的坐标;
的坐标;
(4)如(图3),在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使三角形
,使三角形![]() 的面积和三角形
的面积和三角形![]() 的面积相等?若存在,求出
的面积相等?若存在,求出![]() 点坐标,若不存在,说明理由.
点坐标,若不存在,说明理由.
【答案】(1)-3,3;(2)45°;(3)(0,![]() );(4)存在,Q点坐标为(0,5)或(0,2);
);(4)存在,Q点坐标为(0,5)或(0,2);
【解析】
(1)根据非负数的性质得a+b=0,b-a-6=0,然后解方程组求出a和b即可得到点A和B的坐标;
(2)由AB∥DE可知∠ODE+∠DFB=180°,得到∠DFB=∠AFO=180°-140°=40°,所以∠FAO=50°,再根据角平分线定义得∠OAN=![]() ∠FAO=25°,∠NDM=
∠FAO=25°,∠NDM=![]() ∠ODE=70°,得到∠DNM=∠ANO=90°-25°=65°,然后根据三角形内角和定理得∠AMD=180°∠DNM-∠NDM=45°;
∠ODE=70°,得到∠DNM=∠ANO=90°-25°=65°,然后根据三角形内角和定理得∠AMD=180°∠DNM-∠NDM=45°;
(3)①连结OB,如图3,设F(0,t),根据△AOF的面积+△BOF的面积=△AOB的面积得到![]() ×3×t+
×3×t+![]() ×t×3=
×t×3=![]() ×3×3,解得t=
×3×3,解得t=![]() ,则可得到F点坐标为(0,
,则可得到F点坐标为(0,![]() );
);
(4)先计算△ABC的面积=![]() ,利用△ABQ的三角形=△AQF的面积+△BQF的面积得到
,利用△ABQ的三角形=△AQF的面积+△BQF的面积得到![]() |y
|y![]() |3+
|3+![]() |y
|y![]() |3=
|3=![]() ,解出y即可.
,解出y即可.
解:(1)∵(a+b)2+|b-a-6|=0,
∴a+b=0,b-a-6=0,
∴a=3,b=3,
故答案为:-3,3;
(2)∵AB∥DE,
∴∠ODE+∠DFB=180°,
∵![]() ,
,
∴∠DFB=∠AFO=180°-140°=40°,
∴∠FAO=50°,
∵![]() 分别平分
分别平分![]() ,
,
∴∠OAN=![]() ∠FAO=25°,∠NDM=
∠FAO=25°,∠NDM=![]() ∠ODE=70°,
∠ODE=70°,
∴∠DNM=∠ANO=90°-25°=65°,
∴∠AMD=180°∠DNM-∠NDM=45°;
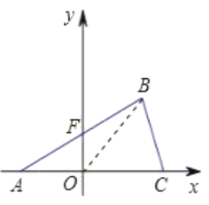
(3)连结OB,如图,
设F(0,t),
∵△AOF的面积+△BOF的面积=△AOB的面积,
∴![]() ×3×t+
×3×t+![]() ×t×3=
×t×3=![]() ×3×3,解得t=
×3×3,解得t=![]() ,
,
∴F点坐标为(0,![]() );
);
(4)存在,
∵![]() ,
,
∴△![]() 的面积=
的面积=![]() ,
,
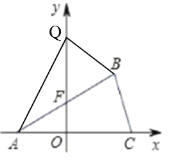
设Q(0,y),
∵△ABQ的三角形=△AQF的面积+△BQF的面积,
∴![]() |y
|y![]() |3+
|3+![]() |y
|y![]() |3=
|3=![]() ,
,
解得y=5或y=2,
∴此时Q点坐标为(0,5)或(0,2);

 名校课堂系列答案
名校课堂系列答案