题目内容
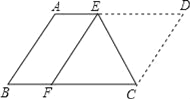
【题目】如图,将ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.
(1)求证:四边形ABFE为平行四边形;
(2)若AB=4,BC=6,求四边形ABFE的周长.
【答案】(1)证明见解析;(2)12.
【解析】
(1)根据折叠的性质得到EF=ED,∠CFE=∠CDE,根据平行四边形的性质得到AD∥BC,∠B=∠D,由平行线的判定得到AE∥BF,即可得到结论;
(2)根据平行四边形的性质得到EF=AB=4.求得ED=4,得到AE=BF=6-4=2,于是得到结论.
(1)证明:∵将ABCD沿CE折叠,使点D落在BC边上的F处,∴EF=ED,∠CFE=∠CDE,
∵四边形ABCD是平行四边形,∴AD∥BC,∠B=∠D,∴AE∥BF,∠B=∠CFE,
∴AB∥EF,∴四边形ABFE为平行四边形;
(2)解:∵四边形ABFE为平行四边形,∴EF=AB=4,
∵EF=ED,∴ED=4,∴AE=BF=6﹣4=2,∴四边形ABFE的周长=AB+BF+EF+EA=12.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目