题目内容
【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
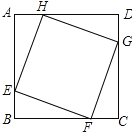
A. 30 B. 34 C. 36 D. 40
【答案】B
【解析】在Rt△AEH中,由勾股定理求出EH=![]() ,根据正方形面积公式求出即可
,根据正方形面积公式求出即可
解: ∵四边形ABCD是正方形, AE=BF=CG=DH, ∴AH=DG=CF=BE,
∴△AEH≌△DHG≌△CGF≌△BFE(SAS),
∴EH=EF=FG=HG,∵∠A=∠D=90°,
∴∠DGH+∠DHG=90°,
∴∠AHE+∠DHG=90°,
∴∠EHG=180°-90°=90°,
∴四边形EFGH是正方形,
在Rt△AEH中,AE=2,AH=5,由勾股定理得:EH=![]() =
=![]() ,
,
∵四边形EFGH是正方形,
∴EF=FG=GH=EH=![]() ,
,
∴四边形EFGH的面积是(![]() )2=34.
)2=34.
故选B.
“点睛”本题考查了正方形性质,全等三角形的性质和判定,三角形内角和定理,正方形判定的应用,关键是推出四边形EFGH是正方形.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目