Question

【题目】某公司经销的一种产品每件成本为40元，要求在90天内完成销售任务．已知该产品90天内每天的销售价格与时间（第x天）的关系如下表：

时间（第x天）	1≤x＜50	50≤x≤90
	x+50	90

任务完成后，统计发现销售员小王90天内日销售量p（件）与时间（第x天）满足一次函数关系p＝﹣2x+200．设小王第x天销售利润为W元．

（1）直接写出W与x之间的函数关系式，井注明自变量x的取值范围；

（2）求小生第几天的销售量最大？最大利润是多少？

（3）任务完成后，统计发现平均每个销售员每天销售利润为4800公司制定如下奖励制度：如果一个销售员某天的销售利润超过该平均值，则该销售员当天可获得200元奖金．请计算小王一共可获得多少元奖金？

Answer 1

【答案】（1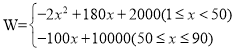）；（2）小王第45天的销售利润最大，最大利润为6050元；（3）小王一共可获得6200元奖金.

【解析】

（1）依据题意销售利润=销售量×（售价-进价）易得出销售利润为W（元）与x（天）之间的函数关系式；

（2）依据（1）中函数的增减性求得最大利润；

（3）根据销售利润为W（元）与x（天）之间的函数关系式，求出利润超过4800元的天数即可求得可获得的奖金金额.

（1）依题意：，

整理得；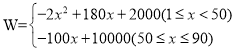

（2）①当1≤x＜50时，W＝﹣2x2+180x+2000＝﹣2（x﹣45）2+6050，

∵﹣2＜0，

∴抛物线开口向下，

∴当x＝45时，W有最大值为6050；

②当50≤x≤90时，W＝﹣100x+10000，

∵﹣100＜0，

∴W随x的增大而减小，

∴当x＝50时，W有最大值为5000，

∵6050＞5000，

∴当x＝45时，W的值最大，最大值为6050，

即小王第45天的销售利润最大，最大利润为6050元；

（3）①当1≤x＜50时，令W＝4800，得W＝﹣2（x﹣45）2+6050＝4800，

解得x1＝20，x2＝70，

∴当W＞4800时，20＜x＜70，

∵1≤x＜50，

∴20＜x＜50；

②当50≤x≤90时，令W＞4800，W＝﹣100x+10000＞4800，

解得x＜52，

∵50≤x≤90，

∴50≤x＜52，

综上所述：当20＜x＜50时，W＞4800，即共有51﹣21+1＝31天的销售利润超过4800元，

∴可获得奖金200×31＝6200元，

即小王一共可获得6200元奖金.