题目内容
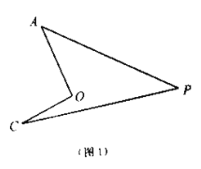
【题目】已知：如图OA平分∠BAC，∠1=∠2．
求证：AO⊥BC．
同学甲说：要作辅助线；
同学乙说：要应用角平分线性质定理来解决：
同学丙说：要应用等腰三角形“三线合一”的性质定理来解决．
请你结合同学们的讨论写出证明过程．
【答案】见解析
【解析】
作OD⊥AB，OE⊥AC，垂足分别为D、E，根据角平分线的性质可得OD=OE，然后根据等角对等边证出OB=OC，然后利用HL证出Rt△ODB≌Rt△OEC，可得∠ABO=∠ACO，再利用等角对等边证出AB=AC，最后根据三线合一即可证出结论．
解：作OD⊥AB，OE⊥AC，垂足分别为D、E
∵AO平分BAC，
∴OD=OE
∵∠1=∠2
∴OB=OC
在Rt△ODB和Rt△OEC中
∴Rt△ODB≌Rt△OEC
∴∠ABO=∠ACO
又∵∠1=∠2
∴∠ABC=∠ACB
∴AB=AC
∵AO平分∠BAC
∴AO⊥BC
练习册系列答案
相关题目
