题目内容
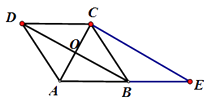
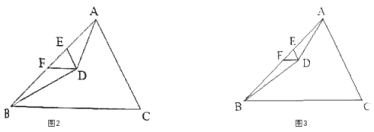
【题目】已知,如图:长方形ABCD中,点E为BC边的中点,将D折起,使点D落在点E处.

(1)请你用尺规作图画出折痕和折叠后的图形.(不要求写已知,求作和作法,保留作图痕迹)
(2)若折痕与AD、BC分别交于点M、N,与DE交于点O,求证△MDO≌△NEO.
【答案】(1)图见解析;(2)证明见解析
【解析】
(1)作DE的垂直平分线分别交AD和BC于点M、N,MN即为折痕,再以E为圆心,CD的长为半径作弧,以N为圆心,NC的长为半径作弧,两弧交于点C′,四边形MEC′N即为四边形MDCN折叠后的图形;
(2)根据矩形的性质可得AD∥BC,从而得出∠MDO=∠NEO,然后根据垂直平分线的定义可得DO=EO,最后利用ASA即可证出结论.
解:(1)分别以D、E为圆心,大于![]() DE的长为半径作弧,两弧分别交于点P、Q,连接PQ,分别交AD和BC于点M、N,连接ME和DN,此时MN垂直平分DE,MN即为折痕;
DE的长为半径作弧,两弧分别交于点P、Q,连接PQ,分别交AD和BC于点M、N,连接ME和DN,此时MN垂直平分DE,MN即为折痕;
再以E为圆心,CD的长为半径作弧,以N为圆心,NC的长为半径作弧,两弧交于点C′,四边形MEC′N即为四边形MDCN折叠后的图形;
(2)∵四边形ABCD为矩形
∴AD∥BC
∴∠MDO=∠NEO
∵MN垂直平分DE
∴DO=EO
在△MDO和△NEO中
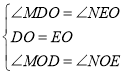
∴△MDO≌△NEO

练习册系列答案
相关题目