题目内容
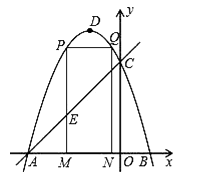
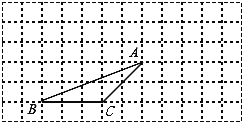
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2 , 请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
【答案】
(1)解:画出△A1B1C与△A2B2C2如图
(2)解:旋转中心的坐标为( ![]() ,-1)
,-1)
(3)解:点P的坐标为(-2,0)
【解析】(1)延长AC到A1 , 使得AC=A1C,延长BC到B1 , 使得BC=B1C,利用点A的对应点A2的坐标为(0,-4),得出图象平移单位,即可得出△A2B2C2。
(2)根据△A1B1C绕某一点旋转可以得到△A2B2C2 , 根据旋转的性质可找出旋转中心。
(3)根据B点关于x轴对称点为A2 , 连接AA2 , 交x轴于点P,再利用相似三角形的性质求出P点坐标即可。

练习册系列答案
相关题目
【题目】谁更合理?
某种牙膏上部圆的直径为2.6cm,下部底边的长为4cm,如图,现要制作长方体的牙膏盒,牙膏盒底面是正方形,在手工课上,小明、小亮、小丽、小芳制作的牙膏盒的高度都一样,且高度符合要求.不同的是底面正方形的边长,他们制作的边长如下表:
制作者 | 小明 | 小亮 | 小丽 | 小芳 |
正方形的边长 | 2cm | 2.6cm | 3cm | 3.4cm |
(1)这4位同学制作的盒子都能装下这种牙膏吗?(![]() )
)
(2)若你是牙膏厂的厂长,从节约材料又方便取放牙膏的角度来看,你认为谁的制作更合理?并说明理由.