题目内容
【题目】给定关于 ![]() 的二次函数
的二次函数 ![]() ,
,
学生甲:当 ![]() 时,抛物线与
时,抛物线与 ![]() 轴只有一个交点,因此当抛物线与
轴只有一个交点,因此当抛物线与 ![]() 轴只有一个交点时,
轴只有一个交点时, ![]() 的值为3;
的值为3;
学生乙:如果抛物线在 ![]() 轴上方,那么该抛物线的最低点一定在第二象限;
轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
【答案】解:甲的观点是错误的.
理由如下:当抛物线 ![]() 与
与 ![]() 轴只有一个交点时
轴只有一个交点时![]()
即: ![]()
解得 ![]() 或
或 ![]()
即 ![]() 或
或 ![]() 时抛物线
时抛物线 ![]() 与
与 ![]() 轴只有一个交点
轴只有一个交点
乙的观点是正确的
理由如下:当抛物线在 ![]() 轴上方时,
轴上方时,
由上可得 ![]()
即: ![]()
∴ ![]()
而对于开口向上的抛物线最低点为其顶点
顶点的横坐标为 ![]()
![]()
![]() ,且抛物线在
,且抛物线在 ![]() 轴上方,
轴上方,
即抛物线的最低点在第二象限
【解析】根据抛物线与 x 轴只有一个交点,得到![]() -4ac=0,可计算m的值,确定甲的观点是错误的.根据抛物线在 x 轴上方,得到
-4ac=0,可计算m的值,确定甲的观点是错误的.根据抛物线在 x 轴上方,得到![]() -4ac
-4ac![]() 0,m的范围可求出,抛物线的最低点的位置即可确定。
0,m的范围可求出,抛物线的最低点的位置即可确定。

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】2020年拟继续举办丽水市中学生汉字听写、诗词诵写大赛.经过初赛、复赛,选出了两个代表队参加市内7月份的决赛.两个队各选出的![]() 名选手的复赛成绩如图所示.
名选手的复赛成绩如图所示.
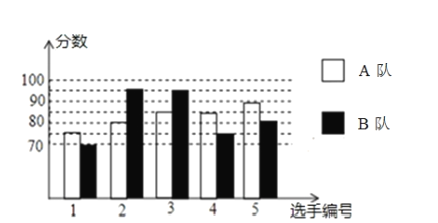
(1)根据图示补全下表;
平均数(分) | 中位数(分) | 众数(分) | |
|
|
| |
|
|
(2)结合两队成绩的平均数和中位数,分析哪个队的复赛成绩较好;
(3)计算两队成绩的方差,并判断哪一个代表队选手成绩较为稳定.