题目内容
【题目】如图(1),已知四边形ABCD的四条边相等,四个内角都等于90°,点E是CD边上一点,F是BC边上一点,且∠EAF=45°.
(1)求证:BF+DE=EF;
(2)若AB=6,设BF=x,DE=y,求y关于x的函数解析式,并写出x的取值范围;
(3)过点A作AH⊥FE于点H,如图(2),当FH=2,EH=1时,求△AFE的面积.

【答案】(1)见解析;(2)y=![]() (0≤x≤6);(3)
(0≤x≤6);(3)![]() .
.
【解析】
(1)如图1中,将△ADE绕点A顺时针旋转90°得到△ABH.只要证明△AFH≌△AFE(SAS)即可解决问题;,
(2)利用(1)中结论,在Rt△ECF中,根据EF2=CF2+EC2,构建关系式即可;
(3)如图2中,将△ADE绕点A顺时针旋转90°得到△ABM.首先证明AH=AB,设AB=x,在Rt△EFC中,利用勾股定理构建方程即可解决问题;
(1)如图1中,将△ADE绕点A顺时针旋转90°得到△ABH,
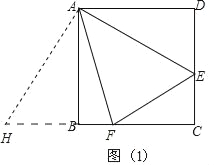
∵四边形ABCD是正方形,
∴AB=AD=CD=BC,∠BAD=90°,
∵∠EAF=45°,
∴∠BAF+∠BAH=∠BAF+∠DAE=45°,
∴∠FAH=∠FAE=45°,
∵AF=AF,AH=AE,
∴△AFH≌△AFE(SAS),
∴EF=FH,
∵FH=BH+BF=DE+BF,
∴EF=BF+DE;
(2)∵AB=BC=CD=6,BF=x,DE=y,
∴EF=x+y,FC=6=﹣x,EC=6﹣y,
在Rt△ECF中,∵EF2=CF2+EC2,
∴(x+y)2=(6﹣x)2+(6﹣y)2,
∴y=![]() (0≤x≤6);
(0≤x≤6);
(3)如图2中,将△ADE绕点A顺时针旋转90°得到△ABM.
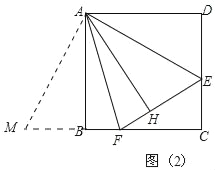
由(1)可知△AFM≌△AFH,
∵AB⊥FM,AH⊥EF,
∴AB=AH,
设AB=BC=CD=AD=x,
∵∠ABF=∠AHF=90°,
∵AF=AF.AB=AH,
∴Rt△AFB≌Rt△AFH(HL),
∴BF=FH=2,同理可证:DE=EH=1,
∴CF=x﹣2,EC=x﹣1,
在Rt△ECF中,∵EF2=CF2+EC2,
∴32=(x﹣2)2+(x﹣1)2,
∴x=![]() 或
或![]() (舍弃),
(舍弃),
∴S△AEF=![]() EFAH=
EFAH=![]() ×3×
×3×![]() =
=![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案