题目内容
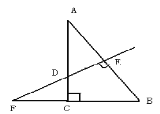
【题目】如图,Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交BC的延长线于F,若∠F=30°,DE=1,则EF的长是_____.
【答案】3
【解析】
如图,连接AF,根据等腰三角形的性质,得到AF=BF,求出∠AFE、∠B,得出∠BAC=30°,求出AD,根据∠FAC=∠AFE=30°,推出AD=DF,代入求出DF,再加上DE即可得到答案.

连接AF,
∵AB的垂直平分线DE交于BC的延长线于F,
∴AF=BF,
∴∠AFE=∠BFE=30°,
∵FE⊥AB,
∴∠B=∠FAB=90°-30°=60°,
∵∠ACB=90°,
∴∠BAC=30°,
∴∠FAC=60°-30°=30°,
∵DE=1,
∴AD=2DE=2,
∵∠FAD=∠AFD=30°,
∴DF=AD=2,
∴EF=DF+DE=3.
故答案为:3.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目