题目内容
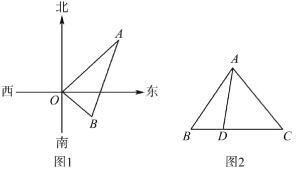
【题目】(1)如图1,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,求水管AB的长;
(2)如图2,在△ABC中,D是BC边上的点,已知AB=13,AD=12,AC=15,BD=5,求DC的长.
【答案】(1)AB的长为40m;(2)CD=9.
【解析】(1)东北方向和东南方向间刚好是一直角,利用勾股定理解图中直角三角形即可;
(2)先根据勾股定理的逆定理判断出△ABD的形状,再根据勾股定理求出CD的长即可.
(1)由题意可得∠AOB=90°,
在Rt△AOB中,
AB=![]() =
=![]() =40(m),
=40(m),
答:水管AB的长为40m;
(2)∵AB=13,AD=12,BD=5,
∴![]()
∴![]() ,
,
∴∠ADB=∠ADC=90°,
在Rt△ADC中,∵AC=15,
∴CD=![]() =9.
=9.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目