题目内容
【题目】甲骑自行车从A地出发，以每小时15km的速度驶向B地，经半小时后乙骑自行车从B地出发，以每小时20km的速度驶向A地，两人相遇时，乙已超过AB两地的中点5km，求A、B两地的距离．
【答案】130km
【解析】
由题目可知：甲的速度为每小时15km，乙的速度为每小时20km，甲先出发半小时后乙才出发，在半小时中甲走的路程为：15×
＝7.5可以设A、B两地相距为xkm，则由题可知两人相距时，乙总共走了(
+5)km，从乙出发到相遇甲走的路程为：(57.5)km，由从乙出发后到甲乙相遇，甲乙所用的时间是相同的可列方程．
由题目设A、B两地相距为xkm，
由分析可知：从乙出发后到甲乙相遇，
甲乙所用的时间是相同的可列方程为：
，
解得：x=130．
所以A、B两地相距为130km．
答：A、B两地相距为130km．
练习册系列答案
相关题目
【题目】某公司装修需用A型板材240块，B型板材180块，A型板材规格是60cm×30cm，B型板材规格是40cm×30cm．现只能购得规格是150cm×30cm的标准板材．一张标准板材尽可能多地裁出A型、B型板材，共有下列三种裁法：（如图是裁法一的裁剪示意图）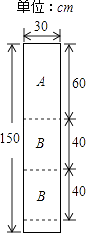 
裁法一 | 裁法二 | 裁法三 | |
A型板材块数 | 1 | 2 | 0 |
B型板材块数 | 2 | m | n |
（1）上表中，m= ， n=；
（2）若裁完剩余的部分可以拼接成A型或B型板材使用，则至少需要几张标准板材？
（3）若裁完剩余的部分不能拼接成A型或B型板材使用，已知用170张标准板材，可以完成装修任务．请通过计算写出两种剪裁方案（要求：①其中一种方案三种剪裁方法都使用，另一种方案只用到两种剪裁方法；②每种方案需写出使用各种裁剪方法裁剪标准板的张数）．
