题目内容
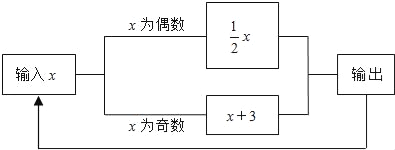
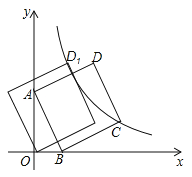
【题目】如图,直线![]() 与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线
与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线![]() (
(![]() )上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线
)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线![]() (
(![]() )上的点D1处,则a= .
)上的点D1处,则a= .
【答案】2.
【解析】
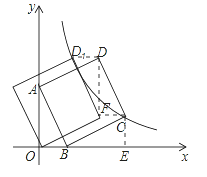
试题对于直线![]() ,令x=0,得到y=3;令y=0,得到x=1,即A(0,3),B(1,0),过C作CE⊥x轴,交x轴于点E,过P作OF∥x轴,过D作DF垂直于OF,如图所示,∵四边形ABCD为正方形,∴AB=BO,∠ABO=90°,∴∠OAB+∠ABO=90°,∠ABO+∠EBO=90°,∴∠OAB=∠EBO,在△AOB和△BEO中,∵∠AOB=∠BEO=90°,∠OAB=∠EBO,AB=BO,∴△AOB≌△EBO(AAS),∴BE=OA=3,OE=OB=1,∴C(4,1),把C坐标代入反比例解析式得:k=4,即
,令x=0,得到y=3;令y=0,得到x=1,即A(0,3),B(1,0),过C作CE⊥x轴,交x轴于点E,过P作OF∥x轴,过D作DF垂直于OF,如图所示,∵四边形ABCD为正方形,∴AB=BO,∠ABO=90°,∴∠OAB+∠ABO=90°,∠ABO+∠EBO=90°,∴∠OAB=∠EBO,在△AOB和△BEO中,∵∠AOB=∠BEO=90°,∠OAB=∠EBO,AB=BO,∴△AOB≌△EBO(AAS),∴BE=OA=3,OE=OB=1,∴C(4,1),把C坐标代入反比例解析式得:k=4,即![]() ,同理得到△DFO≌△AOB,∴DF=OA=3,OF=OB=1,∴D(3,4),把y=4代入反比例解析式得:x=1,则将正方形ABCD沿x轴负方向平移2个单位长度,使点D恰好落在双曲线
,同理得到△DFO≌△AOB,∴DF=OA=3,OF=OB=1,∴D(3,4),把y=4代入反比例解析式得:x=1,则将正方形ABCD沿x轴负方向平移2个单位长度,使点D恰好落在双曲线![]() (
(![]() )上的点D1处,即a=2,故答案为:2.
)上的点D1处,即a=2,故答案为:2.

练习册系列答案
相关题目