题目内容
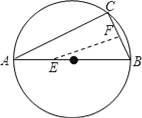
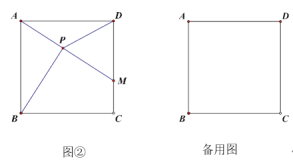
【题目】(1)如图①,已知正方形ABCD的边长是4,M在DC上,M是CD的中点,点P是AC边上的一动点,则当DP+MP的值最小时,在备用图(答题卷上)中用尺规作出点P的位置,并直接写出DP的长是?
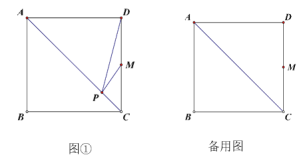
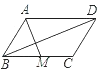
(2)如图②,已知正方形ABCD的边长是4,点M是DC上的一个动点,连结AM,作BP⊥AM于点P,连结DP,当DP最小时,在备用图(答题卷上)中用尺规作出点P的位置,并直接写出DP的长是?
【答案】(1)见解析,![]() ;(2)见解析,
;(2)见解析,![]()
【解析】
(1)作点M关于BC的对称点M′,连结DM′交AC于点P,此时DP+MP最小,最小值为DM′,根据勾股定理求得DM′,然后根据三角形相似对应边成比例即可求得DP;
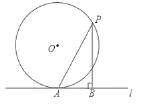
(2)以AB为直径作△APB的内接圆,当DP最小时,N、P、D三点共线,DP最小,根据勾股定理求得ND=
5 |
,即可求得DP.
(1)如图1①,
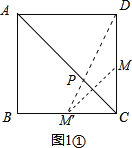
作点M关于BC的对称点M′,连结DM′交AC于点P,
此时DP+MP最小,最小值为DM′,
DM′=![]() ,
,
∵AD∥BC,
△ADP∽△CM′P,
∴DP:PM′=AD:CM′=2:1
∴![]() ;
;
(2)如图②正方形ABCD边长是4,所以三角形ABP的半径是2,DN长是2![]() .DP最小是
.DP最小是![]() .
.
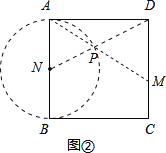
∵BP⊥AM,
∴△ABP是直角三角形,
∴以AB为直径作△APB的外接圆,
∵正方形ABCD边长是4,
∴三角形ABP的半径是2,DN长是2![]() .
.
当DP最小时,N、P、D三点共线
∴DP最小值=2![]() -2.
-2.

【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?