Question

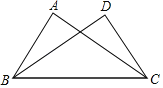
【题目】如图，平行四边形ABCD中，M是BC的中点，且AM=9，BD=12，AD=10，则ABCD的面积是（　　）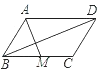

A. 30B. 36C. 54D. 72

Answer 1

【答案】D

【解析】

求ABCD的面积，就需求出BC边上的高，可过D作DE∥AM，交BC的延长线于E，那么四边形ADEM也是平行四边形，则AM=DE；在△BDE中，三角形的三边长正好符合勾股定理的逆定理，因此△BDE是直角三角形；可过D作DF⊥BC于F，根据三角形面积的不同表示方法，可求出DF的长，也就求出了BC边上的高，由此可求出四边形ABCD的面积．

作DE∥AM，交BC的延长线于E，则ADEM是平行四边形，

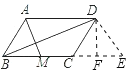
∴DE=AM=9，ME=AD=10，
又由题意可得，BM=BC=

AD=5，则BE=15，
在△BDE中，∵BD2+DE2=144+81=225=BE2，
∴△BDE是直角三角形，且∠BDE=90°，
过D作DF⊥BE于F，
则DF=，
∴SABCD=BCFD=10×=72．
故选D．