ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕуЕНжБЯпЕФОрРыМДЮЊЕуЕНжБЯпЕФДЙЯпЖЮЕФГЄЃЎ
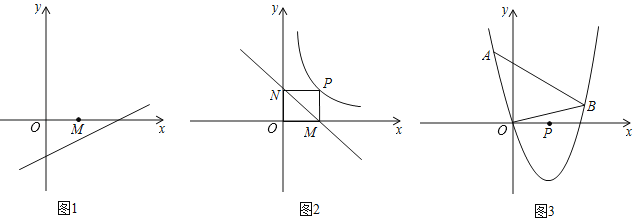
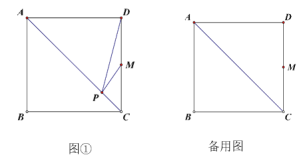
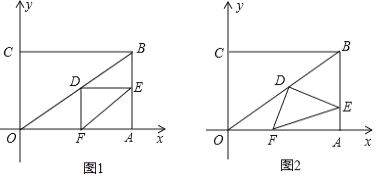
ЃЈ1ЃЉШчЭМ1ЃЌШЁЕуMЃЈ1ЃЌ0ЃЉЃЌдђЕуMЕНжБЯпlЃКyЃН![]() xЉ1ЕФОрРыЮЊЖрЩйЃП
xЉ1ЕФОрРыЮЊЖрЩйЃП
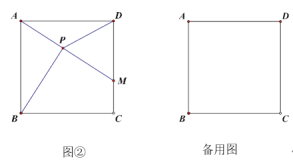
ЃЈ2ЃЉШчЭМ2ЃЌЕуPЪЧЗДБШР§КЏЪ§yЃН![]() дкЕквЛЯѓЯоЩЯЕФвЛИіЕуЃЌЙ§ЕуPЗжБ№зїPMЁЭxжсЃЌзїPNЁЭyжсЃЌМЧPЕНжБЯпMNЕФОрРыЮЊd0ЃЌЮЪЪЧЗёДцдкЕуPЃЌЪЙd0ЃН
дкЕквЛЯѓЯоЩЯЕФвЛИіЕуЃЌЙ§ЕуPЗжБ№зїPMЁЭxжсЃЌзїPNЁЭyжсЃЌМЧPЕНжБЯпMNЕФОрРыЮЊd0ЃЌЮЪЪЧЗёДцдкЕуPЃЌЪЙd0ЃН![]() ЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
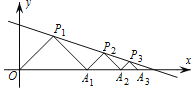
ЃЈ3ЃЉШчЭМ3ЃЌШєжБЯпyЃНkx+mгыХзЮяЯпyЃНx2Љ4xЯрНЛгкxжсЩЯЗНСНЕуAЁЂBЃЈAдкBЕФзѓБпЃЉЃЎЧвЁЯAOBЃН90ЁуЃЌЧѓЕуPЃЈ2ЃЌ0ЃЉЕНжБЯпyЃНkx+mЕФОрРызюДѓЪБЃЌжБЯпyЃНkx+mЕФНтЮіЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЕуPЃЈ
ЃЛЃЈ2ЃЉЕуPЃЈ![]() ЃЌ2
ЃЌ2![]() ЃЉЛђЃЈ2
ЃЉЛђЃЈ2![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉyЃНЉ2x+9
ЃЉЃЛЃЈ3ЃЉyЃНЉ2x+9
ЁОНтЮіЁП
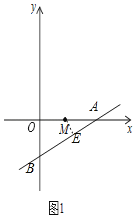
ЃЈ1ЃЉШчЭМ1ЃЌЩшжБЯпlЃКyЃН![]() xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЙ§ЕуMзїMEЁЭABЃЌЯШЧѓГіЕуAЃЌЕуBзјБъЃЌПЩЕУOAЃН2ЃЌOBЃН1ЃЌAMЃН1ЃЌгЩЙДЙЩЖЈРэПЩЧѓABГЄЃЌгЩШёНЧШ§НЧКЏЪ§ПЩЧѓНтЃЛ
xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЙ§ЕуMзїMEЁЭABЃЌЯШЧѓГіЕуAЃЌЕуBзјБъЃЌПЩЕУOAЃН2ЃЌOBЃН1ЃЌAMЃН1ЃЌгЩЙДЙЩЖЈРэПЩЧѓABГЄЃЌгЩШёНЧШ§НЧКЏЪ§ПЩЧѓНтЃЛ
ЃЈ2ЃЉЩшЕуPЃЈaЃЌ![]() ЃЉЃЌгУВЮЪ§aБэЪОMNЕФГЄЃЌгЩУцЛ§ЙиЯЕПЩЧѓaЕФжЕЃЌМДПЩЧѓЕуPзјБъЃЛ
ЃЉЃЌгУВЮЪ§aБэЪОMNЕФГЄЃЌгЩУцЛ§ЙиЯЕПЩЧѓaЕФжЕЃЌМДПЩЧѓЕуPзјБъЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭyжсгкЕуDЃЌЩшЕуAЃЈaЃЌa2Љ4aЃЉЃЌЕуBЃЈbЃЌb2Љ4bЃЉЃЌЭЈЙ§жЄУїЁїAOCЁзЁїBODЃЌПЩЕУabЉ4ЃЈa+bЃЉ+17ЃН0ЃЌгЩИљгыЯЕЪ§ЙиЯЕПЩЧѓa+bЃНk+4ЃЌabЃНЉmЃЌПЩЕУyЃНkx+1Љ4kЃНkЃЈxЉ4ЃЉ+1ЃЌПЩЕУжБЯпyЃНkЃЈxЉ4ЃЉ+1Й§ЖЈЕуNЃЈ4ЃЌ1ЃЉЃЌдђЕБPNЁЭжБЯпyЃНkx+mЪБЃЌЕуPЕНжБЯпyЃНkx+mЕФОрРызюДѓЃЌгЩД§ЖЈЯЕЪ§ЗЈПЩЧѓжБЯпPNЕФНтЮіЪНЃЌПЩЧѓkЃЌmЕФжЕЃЌМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌЩшжБЯпlЃКyЃН![]() xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЙ§ЕуMзїMEЁЭABЃЌ
xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЙ§ЕуMзїMEЁЭABЃЌ
ЁпжБЯпlЃКyЃН![]() xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌ
xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌ
ЁрЕуAЃЈ2ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌЉ1ЃЉЃЌЧвЕуMЃЈ1ЃЌ0ЃЉЃЌ
ЁрAOЃН2ЃЌBOЃН1ЃЌAMЃНOMЃН1ЃЌ
ЁрABЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпtanЁЯOABЃНtanЁЯMAEЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрMEЃН![]() ЃЌ
ЃЌ
ЁрЕуMЕНжБЯпlЃКyЃН![]() xЉ1ЕФОрРыЮЊ
xЉ1ЕФОрРыЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшЕуPЃЈaЃЌ![]() ЃЉЃЌЃЈaЃО0ЃЉ
ЃЉЃЌЃЈaЃО0ЃЉ
ЁрOMЃНaЃЌONЃН![]() ЃЌ
ЃЌ
ЁрMNЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпPMЁЭxжсЃЌPNЁЭyжсЃЌЁЯMONЃН90ЁуЃЌ
ЁрЫФБпаЮPMONЪЧОиаЮЃЌ
ЁрSЁїPMNЃН![]() SОиаЮPMONЃН2ЃЌ
SОиаЮPMONЃН2ЃЌ
Ёр![]() ЁСMNЁСd0ЃН2ЃЌ
ЁСMNЁСd0ЃН2ЃЌ
Ёр![]() ЁС
ЁС![]() ЃН4ЃЌ
ЃН4ЃЌ
Ёрa4Љ10a2+16ЃН0ЃЌ
Ёрa1ЃН2ЃЌa2ЃНЉ2ЃЈЩсШЅЃЉЃЌa3ЃН2![]() ЃЌa4ЃНЉ2
ЃЌa4ЃНЉ2![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрЕуPЃЈ![]() ЃЌ2
ЃЌ2![]() ЃЉЛђЃЈ2
ЃЉЛђЃЈ2![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЃЈ3ЃЉШчЭМ3ЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭyжсгкЕуDЃЌ
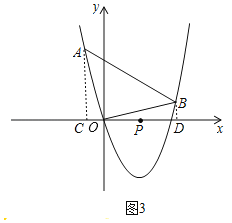
ЩшЕуAЃЈaЃЌa2Љ4aЃЉЃЌЕуBЃЈbЃЌb2Љ4bЃЉЃЌ
ЁпЁЯAOBЃН90ЁуЃЌ
ЁрЁЯAOC+ЁЯBODЃН90ЁуЃЌЧвЁЯAOC+ЁЯCAOЃН90ЁуЃЌ
ЁрЁЯBODЃНЁЯCAOЃЌЧвЁЯACOЃНЁЯBDOЃЌ
ЁрЁїAOCЁзЁїBODЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
ЁрabЉ4ЃЈa+bЃЉ+17ЃН0ЃЌ
ЁпжБЯпyЃНkx+mгыХзЮяЯпyЃНx2Љ4xЯрНЛгкxжсЩЯЗНСНЕуAЁЂBЃЌ
ЁрaЃЌbЪЧЗНГЬkx+mЃНx2Љ4xЕФСНИљЃЌ
Ёрa+bЃНk+4ЃЌabЃНЉmЃЌ
ЁрЉmЉ4ЃЈk+4ЃЉ+17ЃН0ЃЌ
ЁрmЃН1Љ4kЃЌ
ЁрyЃНkx+1Љ4kЃНkЃЈxЉ4ЃЉ+1ЃЌ
ЁржБЯпyЃНkЃЈxЉ4ЃЉ+1Й§ЖЈЕуNЃЈ4ЃЌ1ЃЉЃЌ
ЁрЕБPNЁЭжБЯпyЃНkx+mЪБЃЌЕуPЕНжБЯпyЃНkx+mЕФОрРызюДѓЃЌ
ЩшжБЯпPNЕФНтЮіЪНЮЊyЃНcx+dЃЌ
Ёр![]()
НтЕУ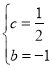
ЁржБЯпPNЕФНтЮіЪНЮЊyЃН![]() xЉ1ЃЌ
xЉ1ЃЌ
ЁрkЃНЉ2ЃЌ
ЁрmЃН1Љ4ЁСЃЈЉ2ЃЉЃН9ЃЌ
ЁржБЯпyЃНkx+mЕФНтЮіЪНЮЊyЃНЉ2x+9ЃЎ