题目内容
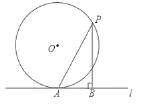
【题目】如图，直线l与半径为2的⊙O相切于点A，P是⊙O上的一个动点（不与点A重合），过点P作PB⊥l，垂足为B，连接PA．设PAPB=m，则m的取值范围是__________．
【答案】
【解析】
作直径AC，连接CP，得出△APC∽△PBA，利用
得出PB=
可求出m最大值是1，点P与点A重合时，PA-PB最小为0，从而求出m的取值范围．
如图，作直径AC，连接CP，
∴∠CPA=90°，
∵AB是切线，
∴CA⊥AB，
∵PB⊥l，
∴AC∥PB，
∴∠CAP=∠APB，
∴△APC∽△PBA，
∴，
∴AP2=PB×PC=8PB
即PB=
PA2．
∴PA-PB=PA-PA2=-（PA-2）2+1
∴当PA=2时，PA-PB最大值为1；
当点P与点A重合时，PA-PB的值最小，为0.
故m的取值范围为：
故答案为：．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
