题目内容
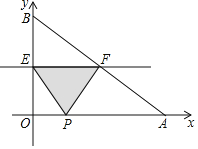
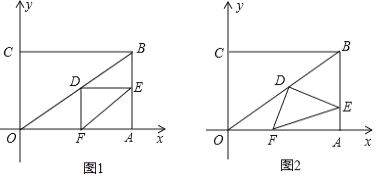
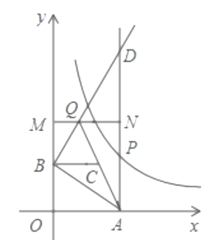
【题目】如图,在平面直角坐标系中,点A(a,0)是x轴正半轴上一点,PA⊥x轴,点B坐标为(0,b)(b>0),动点M在y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
(1)若a=2b,点D坐标为(m,n),求![]() 的值;
的值;
(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为![]() ,求经过点B,Q两点的直线解析式;
,求经过点B,Q两点的直线解析式;
(3)当点Q在射线BD上时,且a3,b1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证明![]() 得
得![]() ,从而得
,从而得![]() ,
,![]() ,故可得m,n的值,进一步可得
,故可得m,n的值,进一步可得![]() 的值;
的值;
(2)由菱形的性质可证明![]() 结合菱形BQNC的面积求出点B、D的坐标,设出直线BD的解析式,将B、D点的坐标代入解析式从而求解即可,
结合菱形BQNC的面积求出点B、D的坐标,设出直线BD的解析式,将B、D点的坐标代入解析式从而求解即可,
(3)分两类进行讨论,当点Q在线段BD上,根据题干条件求出AQ的长,进而求出四边形的周长,当点Q在线段BD的延长线上,依然根据题干条件求出AQ的长,再进一步求出四边形的周长.
(1)![]() ,
,![]() 轴
轴
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,
![]() ,
,![]()
![]()
(2)如图,
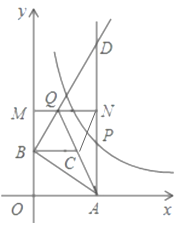
![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() ,
,![]() .
.
![]() ,
,![]() 是
是![]() 的中点,
的中点,
![]() .
.
![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,
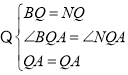 ,
,
![]() .
.
![]()
![]() .
.
![]() 四边形
四边形![]() ,
,
![]() .
.
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
设经过点![]() ,
,![]() 两点的直线解析式为y=kx+b,
两点的直线解析式为y=kx+b,
把![]() ,
,![]() 代入解析式得,
代入解析式得,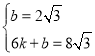 ,
,
解得,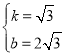
∴经过点![]() ,
,![]() 两点的直线解析式为:
两点的直线解析式为:![]()
(3)![]() ,
,![]() ,
,
![]() .
.
∵DA⊥x轴,
∴DA//y轴,
∴∠DAB=∠ABO,
又∠AOB=∠DBA
![]() ,
,
![]() .
.
![]() .
.
①如图,当点![]() 在线段
在线段![]() 上,
上,
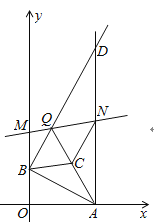
![]() ,
,![]() 为
为![]() 的中点,
的中点,
![]() .
.
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() 四边形
四边形![]() .
.
②如图,当点![]() 在线段
在线段![]() 的延长线上,
的延长线上,
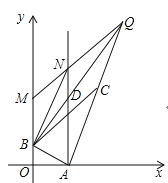
![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() .
.
![]() .
.
![]() .
.
![]()
![]() 平行四边形
平行四边形![]() .
.

【题目】公历3月12日是植树节,为宣传保护数目,激发人们爱林造林的热情,政府投资13万元给某村民小组用于购买与种植![]() 两种树苗共3000棵,完成这项种植后,剩余的款项作为村民小组的纯收入,已知用160元购买
两种树苗共3000棵,完成这项种植后,剩余的款项作为村民小组的纯收入,已知用160元购买![]() 树苗比购买
树苗比购买![]() 树苗多3棵,这两种树苗的单价、成活率及移栽费用见下表:
树苗多3棵,这两种树苗的单价、成活率及移栽费用见下表:
(1)求表中![]() 的值;
的值;
(2)设购买![]() 树苗
树苗![]() 棵,其它购买的是
棵,其它购买的是![]() 树苗,把这些树苗种植完成后,村民小组获得的纯收入为
树苗,把这些树苗种植完成后,村民小组获得的纯收入为![]() 元,请你写出
元,请你写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若要求这批树苗种植后,成活率达到93%以上(包含93%),则最多种植![]() 树苗多少棵?此时,村民小组在这项工作中,所得的纯收入最大值可以是多少元?
树苗多少棵?此时,村民小组在这项工作中,所得的纯收入最大值可以是多少元?
树苗品种 |
|
|
购买价格(元/棵) |
|
|
树苗成活率 | 90% | 95% |
移栽费用(元/棵) | 3 | 5 |