题目内容
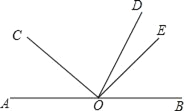
【题目】如图，在正方形ABCD中，点M在CD边上，点N在正方形ABCD外部，且满足∠CMN＝90°，CM＝MN．连接AN，CN，取AN的中点E，连接BE，AC，交于F点．
（1） ①依题意补全图形；
②求证：BE⊥AC．
（2）请探究线段BE，AD，CN所满足的等量关系，并证明你的结论．
（3）设AB＝1，若点M沿着线段CD从点C运动到点D，则在该运动过程中，线段EN所扫过的面积为______________（直接写出答案）．
【答案】（1）①补图见解析；②证明见解析；（2）2BE＝
AD＋CN，证明见解析；（3）
.
【解析】（1）①依照题意补全图形即可；②连接CE，由正方形以及等腰直角三角形的性质可得出∠ACD=∠MCN=45°，从而得出∠ACN=90°，再根据直角三角形的性质以及点E为AN的中点即可得出AE=CE，由此即可得出B、E在线段AC的垂直平分线上，由此即可证得BE⊥AC；
（2）BE=
AD+
CN．根据正方形的性质可得出BF=AD，再结合三角形的中位线性质可得出EF=CN，由线段间的关系即可证出结论；
（3）找出EN所扫过的图形为四边形DFCN．根据正方形以及等腰直角三角形的性质可得出BD∥CN，由此得出四边形DFCN为梯形，再由AB=1，可算出线段CF、DF、CN的长度，利用梯形的面积公式即可得出结论．
（1）①依题意补全图形，如图1所示．
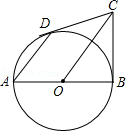
②证明：连接CE，如图2所示．
∵四边形ABCD是正方形，
∴∠BCD=90°，AB=BC，
∴∠ACB=∠ACD=∠BCD=45°，
∵∠CMN=90°，CM=MN，
∴∠MCN=45°，
∴∠ACN=∠ACD+∠MCN=90°．
∵在Rt△ACN中，点E是AN中点，
∴AE=CE=AN．
∵AE=CE，AB=CB，
∴点B，E在AC的垂直平分线上，
∴BE垂直平分AC，
∴BE⊥AC．
（2）BE=AD+CN．
证明：∵AB=BC，∠ABE=∠CBE，
∴AF=FC．
∵点E是AN中点，
∴AE=EN，
∴FE是△ACN的中位线．
∴FE=CN．
∵BE⊥AC，
∴∠BFC=90°，
∴∠FBC+∠FCB=90°．
∵∠FCB=45°，
∴∠FBC=45°，
∴∠FCB=∠FBC，
∴BF=CF．
在Rt△BCF中，BF2+CF2=BC2，
∴BF=BC．
∵四边形ABCD是正方形，
∴BC=AD，
∴BF=AD．
∵BE=BF+FE，
∴BE=AD+CN．
（3）在点M沿着线段CD从点C运动到点D的过程中，线段EN所扫过的图形为四边形DFCN．
∵∠BDC=45°，∠DCN=45°，
∴BD∥CN，
∴四边形DFCN为梯形．
∵AB=1，
∴CF=DF=BD=，CN=CD=，
∴S梯形DFCN=（DF+CN）CF=（+）×=．
