题目内容
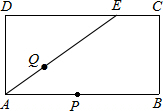
如图,矩形ABCD中,AB=6cm,AD=3cm,点E在边DC上,且DE=4cm.动点P从点A开始沿着A?B?C?E的路线以2cm/s的速度移动,动点Q从点A开始沿着AE以1cm/s的速度移动,当点Q移动到点E时,点P停止移动.若点P、Q同时从点A同时出发,设点Q移动时间为t(s),P、Q两点运动路线与线段PQ围成的图形面积为S(cm2),求S与t的函数关系式.

在Rt△ADE中,AE=
=
=5.(1分)
①当0<t≤3时,如图1.(2分)
过点Q作QM⊥AB于M,连接QP.
∵AB∥CD,∴∠QAM=∠DEA,
又∵∠AMQ=∠D=90°,∴△AQM∽△EAD.
∴
=
,∴QM=
=
t.(3分)
S=
AP•QM=
×2t×
t=
t2.(4分)
②当3<t≤
时,如图2.(5分)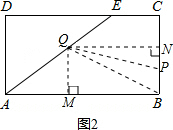
在Rt△ADE中,AE=
=
=5
过点Q作QM⊥AB于M,QN⊥BC于N,连接QB、QP.
∵AB∥CD,∴∠QAM=∠DEA,
又∵∠AMQ=∠ADE=90°,∴△AQM∽△EAD.
∴
=
,
=
,
∴QM=
=
t.(6分)
AM=
=
t,∴QN=BM=6-AM=6-
t.(7分)
∴S△QAB=
AB•QM=
×6×
t=
t
S△QBP=
BP•QN=
(2t-6)(6-
t)=-
t2+
t-18
∴S=S△QAB+S△QBP=
t+(-
t2+
t-18)=-
t2+
t-18(8分)
③当
<t≤5时.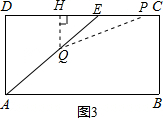
方法1:过点Q作QH⊥CD于H,连接QP.如图3.
由题意得QH∥AD,∴△EHQ∽△EDA,∴
=
∴QH=
=
(5-t)(10分)
∴S梯ABCE=
(EC+AB)•BC=
(2+6)×3=12
S△EQP=
EP•QH=
(11-2t)×
(5-t)=
t2-
t+
∴S=S梯ABCE-S△EQP=12-
t2+
t-
=-
t2+
t-
.(11分)
| AD2+DE2 |
| 32+42 |
①当0<t≤3时,如图1.(2分)
过点Q作QM⊥AB于M,连接QP.
∵AB∥CD,∴∠QAM=∠DEA,
又∵∠AMQ=∠D=90°,∴△AQM∽△EAD.
∴
| QM |
| AD |
| AQ |
| AE |
| AD•AQ |
| AE |
| 3 |
| 5 |
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
②当3<t≤
| 9 |
| 2 |

在Rt△ADE中,AE=
| AD2+DE2 |
| 32+42 |
过点Q作QM⊥AB于M,QN⊥BC于N,连接QB、QP.
∵AB∥CD,∴∠QAM=∠DEA,
又∵∠AMQ=∠ADE=90°,∴△AQM∽△EAD.
∴
| QM |
| AD |
| AQ |
| AE |
| AM |
| DE |
| AQ |
| AE |
∴QM=
| AD•AQ |
| AE |
| 3 |
| 5 |
AM=
| DE•AQ |
| AE |
| 4 |
| 5 |
| 4 |
| 5 |
∴S△QAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 9 |
| 5 |
S△QBP=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 4 |
| 5 |
| 42 |
| 5 |
∴S=S△QAB+S△QBP=
| 9 |
| 5 |
| 4 |
| 5 |
| 42 |
| 5 |
| 4 |
| 5 |
| 51 |
| 5 |
③当
| 9 |
| 2 |

方法1:过点Q作QH⊥CD于H,连接QP.如图3.
由题意得QH∥AD,∴△EHQ∽△EDA,∴
| QH |
| AD |
| QE |
| AE |
∴QH=
| AD•QE |
| AE |
| 3 |
| 5 |
∴S梯ABCE=
| 1 |
| 2 |
| 1 |
| 2 |
S△EQP=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
| 63 |
| 10 |
| 33 |
| 2 |
∴S=S梯ABCE-S△EQP=12-
| 3 |
| 5 |
| 63 |
| 10 |
| 33 |
| 2 |
| 3 |
| 5 |
| 63 |
| 10 |
| 9 |
| 2 |


练习册系列答案
相关题目
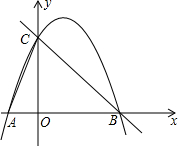 轴的另一个交点.
轴的另一个交点. 

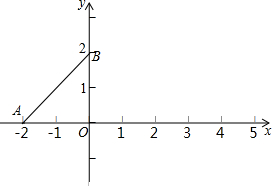 OC,(点A旋转到点B的位置),抛物线y=ax2+bx+c(a≠0)经过B,C两点,与x轴的另一个交点为点D,顶点为点P,对称轴为直线x=3,
OC,(点A旋转到点B的位置),抛物线y=ax2+bx+c(a≠0)经过B,C两点,与x轴的另一个交点为点D,顶点为点P,对称轴为直线x=3,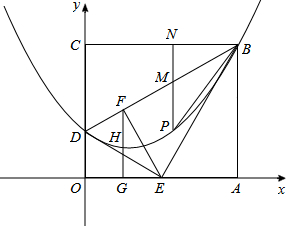
 在抛物线与x轴围成的区域里.
在抛物线与x轴围成的区域里.