题目内容
【题目】在平面直角坐标系xOy中,若点P和点![]() 关于y轴对称,点
关于y轴对称,点![]() 和点
和点![]() 关于直线l对称,则称点
关于直线l对称,则称点![]() 是点P关于y轴,直线l的二次对称点.
是点P关于y轴,直线l的二次对称点.
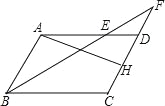
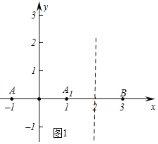
![]() 如图1,点
如图1,点![]() .
.
![]() 若点B是点A关于y轴,直线
若点B是点A关于y轴,直线![]() :
:![]() 的二次对称点,则点B的坐标为______;
的二次对称点,则点B的坐标为______;
![]() 若点
若点![]() 是点A关于y轴,直线
是点A关于y轴,直线![]() :
:![]() 的二次对称点,则a的值为______;
的二次对称点,则a的值为______;
![]() 若点
若点![]() 是点A关于y轴,直线
是点A关于y轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为______;
的表达式为______;
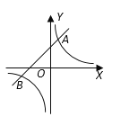
![]() 如图2,
如图2,![]() 的半径为
的半径为![]() 若
若![]() 上存在点M,使得点
上存在点M,使得点![]() 是点M关于y轴,直线
是点M关于y轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,b的取值范围是______;
上,b的取值范围是______;
![]() 是x轴上的动点,
是x轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点N,使得点
上存在点N,使得点![]() 是点N关于y轴,直线
是点N关于y轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在y轴上,求t的取值范围.
在y轴上,求t的取值范围.
【答案】(1)①B(3,0);②a=-2;③y=-x+2;(2)![]() ;(3)
;(3)![]() .
.
【解析】
![]() 根据二次对称点的定义,分别画出图形,即可解决问题.
根据二次对称点的定义,分别画出图形,即可解决问题.
![]() 根据二次对称点的定义,画出图形,求出b的最大值以及最小值即可解决问题.
根据二次对称点的定义,画出图形,求出b的最大值以及最小值即可解决问题.
![]() 如图6中,设点E关于y轴的对称点为
如图6中,设点E关于y轴的对称点为![]() ,
,![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,易知当点N在
,易知当点N在![]() 上运动时,点
上运动时,点![]() 在
在![]() 上运动,由此可见当
上运动,由此可见当![]() 与y轴相切或相交时满足条件
与y轴相切或相交时满足条件![]() 想办法求出点
想办法求出点![]() 的坐标即可解决问题.
的坐标即可解决问题.
解:![]() 如图1中,点
如图1中,点![]() 关于y轴的对称点
关于y轴的对称点![]() ,
,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() .
.
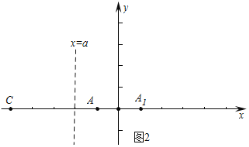
![]() 如图2中,由题意
如图2中,由题意![]() ,
,![]() ,
,![]() 、C关于直线
、C关于直线![]() 对称,
对称,![]() .
.
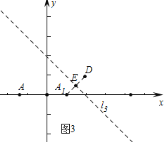
![]() 如图3中,
如图3中,![]() ,
,![]() ,
,![]() 直线
直线![]() 的解析式为
的解析式为![]() ,线段
,线段![]() 的中垂线的解析式为
的中垂线的解析式为![]() ,
,![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
故答案分别为![]() ,
,![]() .
.![]() 如图4中,
如图4中,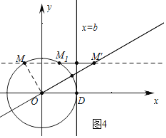
由题意![]() ,由此可知,当
,由此可知,当![]() 的值最大时,可得b的最大值,
的值最大时,可得b的最大值,![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,![]() ,
,![]() ,易知,
,易知,![]() 时,
时,![]() 的值最大,最大值为2,
的值最大,最大值为2,![]() 的最大值为1,
的最大值为1,
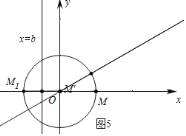
如图5中,易知当点M在x轴的正半轴上时,可得b的最小值,最小值为![]() ,
,
综上所述,满足条件的b取值范围为![]() .
.
故答案为![]() .
.![]() 如图6中,设点E关于y轴的对称点为
如图6中,设点E关于y轴的对称点为![]() ,
,![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,易知当点N在
,易知当点N在![]() 上运动时,点
上运动时,点![]() 在
在![]() 上运动,由此可见当
上运动,由此可见当![]() 与y轴相切或相交时满足条件.
与y轴相切或相交时满足条件.
连接![]() 交直线
交直线![]() 于K,易知直线
于K,易知直线![]() 的解析式为
的解析式为![]() ,
,
由 解得
解得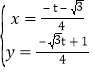 ,
,![]() ,
,![]() ,
,![]() ,
,
当![]() 与y轴相切时,
与y轴相切时,![]() ,解得
,解得![]() 或
或![]() ,
,
综上所述,满足条件的t的取值范围为![]() .
.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案