题目内容
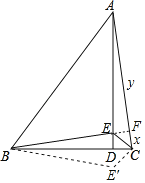
【题目】如图,△ABC中,∠BAC=45°,AD⊥BC于D,点E在AD上,∠BEC=135°,若BC=5,S△ECA=2,则BD=_____.

【答案】![]()
【解析】
如图,延长BE交AC于F,作E关于BC的对称点E′,连接BE′,CE′,则△BE′C≌△BEC,得到∠BE′C=∠BEC=135![]() ,推出点A,B,E′,C四点共圆,根据圆周角定理得到∠E′BC=∠E′AC,求得AF=BF,得到EF=FC,设EF=FC=x,BF=AF=y,解方程组得到y=
,推出点A,B,E′,C四点共圆,根据圆周角定理得到∠E′BC=∠E′AC,求得AF=BF,得到EF=FC,设EF=FC=x,BF=AF=y,解方程组得到y=![]() =
=![]() ,求得BE=y﹣x=3
,求得BE=y﹣x=3![]() ,根据勾股定理得到AE=
,根据勾股定理得到AE=![]() =5,根据相似三角形的性质即可得到结论.
=5,根据相似三角形的性质即可得到结论.
解:如图,延长BE交AC于F,作E关于BC的对称点E′,连接BE′,CE′,则△BE′C≌△BEC,
∴∠BE′C=∠BEC=135![]() ,
,
∵∠BAC=45![]() ,
,
∴∠BAC+∠BE′C=180![]() ,
,
∴点A,B,E′,C四点共圆,
∴∠E′BC=∠E′AC,
∵∠EBC=∠E′BC,
∴∠EBC=∠E′AC,
∵∠BED=∠AEF,
∴∠AFE=∠ADB=90![]() ,
,
∴AF=BF,
∵∠FEC=45![]() ,
,
∴EF=FC,
设EF=FC=x,BF=AF=y,
∴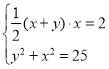 ,
,
解得:x=![]() (负值舍去),x=4(不合题意舍去),
(负值舍去),x=4(不合题意舍去),
∴y=![]() =
=![]() ,
,
∴BE=y﹣x=3![]() ,
,
∴AE=![]() =5,
=5,
∵△BDE∽△AFE,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴BD=![]() ,
,
故答案为:![]() .
.

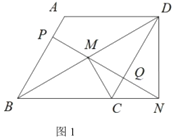
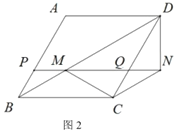
【题目】如图,在![]() 中
中![]() ,
,![]() ,
,![]() 点P从点B出发,沿折线
点P从点B出发,沿折线![]() 运动,当它到达点A时停止,设点P运动的路程为
运动,当它到达点A时停止,设点P运动的路程为![]() 点Q是射线CA上一点,
点Q是射线CA上一点,![]() ,连接
,连接![]() 设
设![]() ,
,![]() .
.
![]() 求出
求出![]() ,
,![]() 与x的函数关系式,并注明x的取值范围;
与x的函数关系式,并注明x的取值范围;
![]() 补全表格中
补全表格中![]() 的值;
的值;
x | 1 | 2 | 3 | 4 | 6 |
| ______ | ______ | ______ | ______ | ______ |
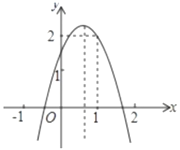
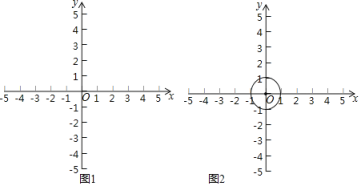
以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点,并在x的取值范围内画出![]() 的函数图象:
的函数图象:
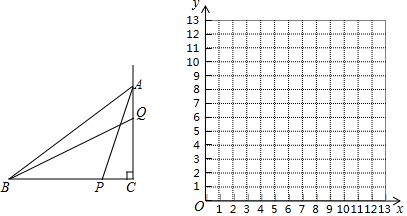
![]() 在直角坐标系内直接画出
在直角坐标系内直接画出![]() 函数图象,结合
函数图象,结合![]() 和
和![]() 的函数图象,求出当
的函数图象,求出当![]() 时,x的取值范围.
时,x的取值范围.