题目内容
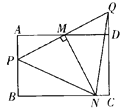
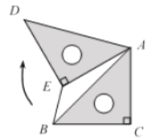
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AC上,DE⊥AB于点E,且CD=DE.点F在BC上,连接EF,AF,若∠CEF=45°,∠B=2∠CAF,BF=2,则AB的长为_____.

【答案】10
【解析】
以AC为轴将△ACF翻至△ACK,在AB边上截取BL=BF=2,设CF=x,则EL=CK=x,分别用含x的式子表示出Rt△ABC中的三边长,根据勾股定理列方程,解得x值,则可得答案.
解:如图,以AC为轴将△ACF翻至△ACK,在AB边上截取BL=BF=2
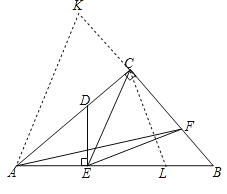
∵∠ACB=90°,DE⊥AB
∴∠BCE+∠DCE=90°,∠BEC+∠DEC=90°
∵CD=DE
∴∠DCE=∠DEC
∴∠BCE=∠BEC
∴BC=BE
∵BF=BL=2
∴EL=CF
设CF=x,则EL=CK=x
∴BK=2x+2,BC=BE=x+2
设∠B=2∠CAF=2α
则∠CAK=α,∠K=90°﹣α
∴∠KAB=180°﹣2α﹣(90°﹣α)=90°﹣α
∴∠K=∠KAB
∴BA=BK=2x+2
在△CBL和△EBF中
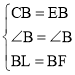
∴△CBL≌△EBF(SAS)
∴∠BCL=∠BEF
又∵∠CEF=45°,∠BCE=∠BEC
∴∠ECL=∠CEF=45°
∴∠ALC=180°﹣45°﹣45°﹣∠BEF=90°﹣∠BEF
∵∠ACL=90°﹣∠BCL,∠BCL=∠BEF
∴∠ALC=∠ACL
∴AC=AL=2x
在Rt△ABC中,由勾股定理得:
(x+2)2+(2x)2=(2x+2)2
解得x=4或x=0(舍)
∴AB=10
故答案为:10.

【题目】今年5月12日是“母亲节”,某校开展“感恩母亲,做点家务”活动为了了解同学们在母亲节这一天做家务情况,学校随机抽查了部分同学,并用得到的数据制成如下不完整的统计表:
做家务时间(小时) | 人数 | 所占百分比 |
| 15 | 30% |
| 31 | 62% |
|
| 4% |
| 2 |
|
合计 |
| 100% |
(1)统计表中的![]() __________,
__________,![]() __________;
__________;
(2)小君计算被抽查同学做家务时间的平均数是这样的:
第一步:计算平均数的公式是![]() ,
,
第二步:该问题中![]() ,
,![]()
![]() ,
,![]() ,
,![]() ;
;
第三步:![]() (小时)
(小时)
小君计算的过程正确吗?如果不正确,请你计算出正确的做家务时间的平均数;
(3)现从![]() ,
,![]() 两组中任选2人,求这2人都在
两组中任选2人,求这2人都在![]() 组中的概率(用树形图法或列表法).
组中的概率(用树形图法或列表法).