Question

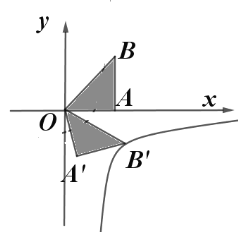
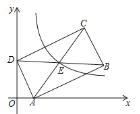
【题目】如图，在平面直角坐标系中，点A的坐标是(2，1)，点B的坐标是(2，0) ．作点B关于OA的对称点B′，则点B′的坐标是______．

Answer 1

【答案】（）

【解析】

连接AB，AB′，BB′，BB′与OA相交于点F，过B′作B′E⊥x轴，垂足为E，由勾股定理求出OA=，再由三角形面积公式可求出BF=， 由对称性得出BB′=，再证明得B′E=，再由勾股定理求出BE=，从而可求出OE=，故可得答案．

连接AB，AB′，BB′，BB′与OA相交于点F，过B′作B′E⊥x轴，垂足为E，如图所示，

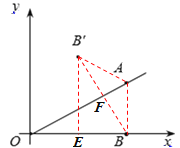
∵点A的坐标是(2，1)，点B的坐标是(2，0) ，

∴OB=2，AB=1，AB⊥OB，

∴AB=

∵

∴

∴

∵点B与点B′关于OA的对称，

∴OA⊥BB′, BB′=2BF=,

又∵B′E⊥x轴，AB⊥OB，

∴B′E//AB

∴∠ABB′=∠BB′E，∠B′EB=∠BFA=90°

∴

∴

∴

∴

∴OE=OB-BE=2-=

∴点B′的坐标为（，）．

故答案为：（，）．