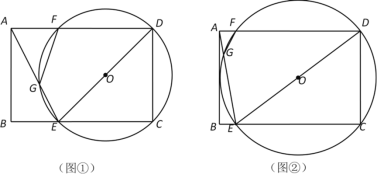题目内容
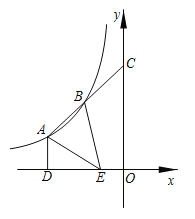
【题目】教材呈现:下图是华师版八年级下册数学教材第11页的部分内容.
例1,如图,在菱形![]() 中,
中,![]() ,试求
,试求![]() 的大小,并说明
的大小,并说明![]() 是等边三角形
是等边三角形
问题解决:请结合图(1),写出例1的完整解答过程;

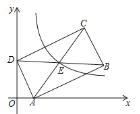
问题探究:在菱形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,过点D作
,过点D作![]() 交BC的延长线于点E.
交BC的延长线于点E.
(1)如图2,连接OE,则OE的长为____________;
(2)如图3,若点P是对角线BD上一动点,连结![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.
【答案】问题解决:见解析;问题探究:(1)![]() ;(2)
;(2)![]()
【解析】
问题解决:根据菱形的性质证明∠ABC=60°即可得证;
问题探究:(1)证明四边形ACED是边长为4的菱形,可得三角形ODE为直角三角形,利用勾股定理即可算出OE的长度;
(2)根据将军饮马问题,可知![]() 的最小值即为AE的长度;
的最小值即为AE的长度;
问题解决:
因为四边形ABCD是菱形,所以![]() ,
,![]()
因为![]()
所以![]()
因为四边形ABCD是菱形, ![]()
所以![]() 是等边三角形;
是等边三角形;
问题探究:
(1)因为四边形ABCD是菱形,所以![]() ,
,
又因为![]() ,所以四边形ACED为平行四边形,由(1)可知AB=AC=AD,所以四边形ACED为菱形,且∠ADE=120°,DE=4,又由菱形的性质可知,∠ADO=30°,AC⊥BD,所以
,所以四边形ACED为平行四边形,由(1)可知AB=AC=AD,所以四边形ACED为菱形,且∠ADE=120°,DE=4,又由菱形的性质可知,∠ADO=30°,AC⊥BD,所以![]() ,∠ODE=120°-30°=90°,利用勾股定理可得
,∠ODE=120°-30°=90°,利用勾股定理可得![]()
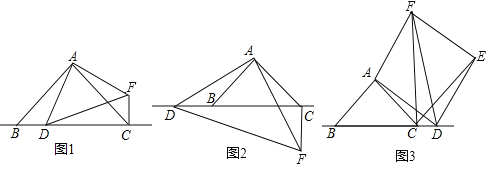
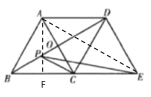
(2)根据将军饮马问题,C点关于BD的对称点为A点,连接AE,AE即为![]() 的最小值,过A作BE的垂线交BE于F,如下图,因为三角形ABC为等边三角形,所以
的最小值,过A作BE的垂线交BE于F,如下图,因为三角形ABC为等边三角形,所以![]() ,FE=6,根据勾股定理可知
,FE=6,根据勾股定理可知![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目