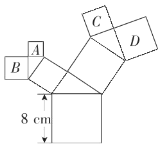
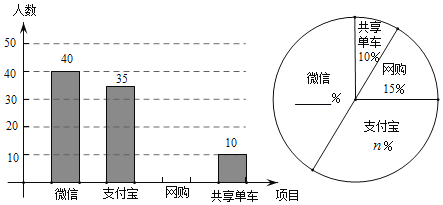
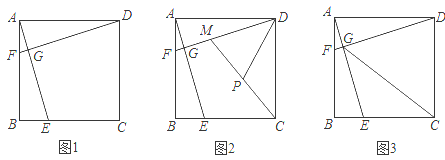
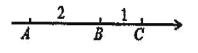题目内容
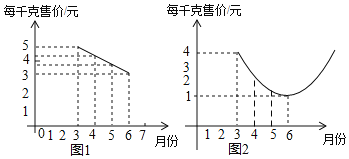
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
【答案】(1)6月份出售这种蔬菜每千克的收益是2元.(2)5月份出售这种蔬菜,每千克的收益最大.(3)4月份的销售量为4万千克,5月份的销售量为6万千克.
【解析】(1)找出当x=6时,y1、y2的值,二者作差即可得出结论;
(2)观察图象找出点的坐标,利用待定系数法即可求出y1、y2关于x的函数关系式,二者作差后利用二次函数的性质即可解决最值问题;
(3)求出当x=4时,y1﹣y2的值,设4月份的销售量为t万千克,则5月份的销售量为(t+2)万千克,根据总利润=每千克利润×销售数量,即可得出关于t的一元一次方程,解之即可得出结论.
(1)当x=6时,y1=3,y2=1,
∵y1﹣y2=3﹣1=2,
∴6月份出售这种蔬菜每千克的收益是2元.
(2)设y1=mx+n,y2=a(x﹣6)2+1.
将(3,5)、(6,3)代入y1=mx+n,
![]() ,解得:
,解得: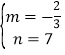 ,
,
∴y1=﹣![]() x+7;
x+7;
将(3,4)代入y2=a(x﹣6)2+1,
4=a(3﹣6)2+1,解得:a=![]() ,
,
∴y2=![]() (x﹣6)2+1=
(x﹣6)2+1=![]() x2﹣4x+13.
x2﹣4x+13.
∴y1﹣y2=﹣![]() x+7﹣(
x+7﹣(![]() x2﹣4x+13)=﹣
x2﹣4x+13)=﹣![]() x2+
x2+![]() x﹣6=﹣
x﹣6=﹣![]() (x﹣5)2+
(x﹣5)2+![]() .
.
∵﹣![]() <0,
<0,
∴当x=5时,y1﹣y2取最大值,最大值为![]() ,
,
即5月份出售这种蔬菜,每千克的收益最大.
(3)当t=4时,y1﹣y2=﹣![]() x2+
x2+![]() x﹣6=2.
x﹣6=2.
设4月份的销售量为t万千克,则5月份的销售量为(t+2)万千克,
根据题意得:2t+![]() (t+2)=22,
(t+2)=22,
解得:t=4,
∴t+2=6.
答:4月份的销售量为4万千克,5月份的销售量为6万千克.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案