题目内容
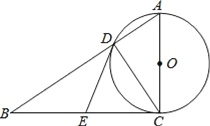
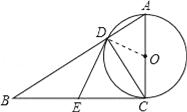
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O,与斜边AB交于点D、E为BC边的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)填空:①若∠B=30°,AC=2![]() ,则DE= ;
,则DE= ;
②当∠B= °时,以O,D,E,C为顶点的四边形是正方形.
【答案】(1)证明就解析;(2)①3;②45.
【解析】试题分析:(1)运用垂径定理、直角三角形的性质证明∠ODE=90°即可解决问题;
(2)①直接利用锐角三角函数关系得出BC的长,再利用直角三角形的性质得出DE的长;
②当∠B=45°时,四边形ODEC是正方形,由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°然后根据有一组邻边相等的矩形是正方形,即可得到结论.
试题解析:(1)连接OD.
∵AC是直径,∴∠ADC=90°,∴∠CDB=90°,
又∵E为BC边的中点,∴DE为直角△DCB斜边的中线,∴DE=CE=![]() .∴∠DCE=∠CDE,
.∴∠DCE=∠CDE,
∵OC=OD,∴∠OCD=∠ODC,∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°,∴∠ODE=90°
∴DE是⊙O的切线.
(2)①∵∠B=30°,AC=2![]() ,∠BCA=90°,∴tan30°=
,∠BCA=90°,∴tan30°=![]() =
=![]() ,解得:BC=6,
,解得:BC=6,
则DE=![]() BC=3;
BC=3;
故答案为:3;
②当∠B=45°时,四边形ODEC是正方形,
∵∠ACB=90°,∴∠A=45°,
∵OA=OD,∴∠ADO=45°,∴∠AOD=90°,∴∠DOC=90°,
∵∠ODE=90°,∴四边形DECO是矩形,
∵OD=OC,∴矩形DECO是正方形.
故答案为:45.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目