题目内容
【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证: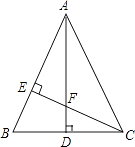
(1)△AEF≌△CEB;
(2)AF=2CD.
【答案】
(1)证明:∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
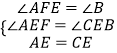 ,
,
∴△AEF≌△CEB(AAS)
(2)证明:∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD
【解析】(1)根据垂直的定义得出∠BCE+∠CFD=90°,∠BCE+∠B=90°,根据同角的余角相等得出∠CFD=∠B,然后由AAS判断出△AEF≌△CEB;
(2)等腰三角形的三线合一得出BC=2CD,根据全等三角形的性质得出AF=BC,从而得出AF=2CD。
【考点精析】关于本题考查的余角和补角的特征和垂线的性质,需要了解互余、互补是指两个角的数量关系,与两个角的位置无关;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短才能得出正确答案.

练习册系列答案
相关题目