题目内容
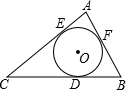
已知Rt△ABC中，∠C=90°，AC=8cm，BC=6cm．则其内心和外心之间的距离是（ ）
| A．10cm | B．5cm | C．
| D．2cm |
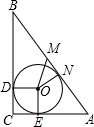
如图，在Rt△ABC，∠C=90°，AC=8cm，BC=6cm，
∴AB=10cm，
∴AM为外接圆半径．
设Rt△ABC的内切圆的半径为r，则OD=OE=r，∠C=90°，
∵四边形OECD是正方形，
∴CE=CD=r，AE=AN=6-r，BD=BN=8-r，
即8-r+6-r=10，
解得r=2cm，
∴AN=4cm；
在Rt△OMN中，
MN=AM-AN=1cm，
OM=
cm．
故选C．
∴AB=10cm，
∴AM为外接圆半径．
设Rt△ABC的内切圆的半径为r，则OD=OE=r，∠C=90°，
∵四边形OECD是正方形，
∴CE=CD=r，AE=AN=6-r，BD=BN=8-r，
即8-r+6-r=10，
解得r=2cm，
∴AN=4cm；
在Rt△OMN中，
MN=AM-AN=1cm，
OM=
| 5 |
故选C．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
