题目内容
【题目】如图,在![]() 中,设
中,设![]() 的对边分别为
的对边分别为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,会有
,会有![]() ,则
,则

![]() ,即
,即![]()
同理![]() ,
,![]()
通过推理还可以得到另一个表达三角形边角关系的定理—余弦定理:

在![]() 中,若
中,若![]() 的对边分别为
的对边分别为![]() ,则
,则
![]()
![]()
![]()
用上面的三角形面积公式和余弦定理解决问题:
(1)如图,在![]() 中,
中,![]() ,
,![]() 的对边分别是3和8.
的对边分别是3和8.

求![]() 和
和![]() .
.
解:![]() _______________;
_______________;
![]() ______________.
______________.
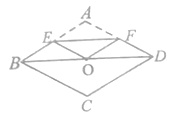
(2)在![]() 中,已知
中,已知![]() ,
,![]() 分别是以
分别是以![]() 为边长的等边三角形,设
为边长的等边三角形,设![]() 的面积分别为
的面积分别为![]() ,求证:
,求证: ![]() .
.

【答案】(1)6![]() ,49;(2)见解析.
,49;(2)见解析.
【解析】
试题分析:(1)直接利用正弦定理和余弦定理即可得出结论;
(2)方法1、利用正弦定理得出三角形的面积公式,再利用等边三角形的性质即可得出结论;
方法2、先用正弦定理得出S1,S2,S3,S4,最后用余弦定理即可得出结论.
试题解析:(1)在△DEF中,∠F=60°,∠D、∠E的对边分别是3和8,
∴EF=3,DF=8,
∴S△DEF=![]() EF×DFsin∠F=
EF×DFsin∠F=![]() ×3×8×sin60°=6
×3×8×sin60°=6![]() ,
,
DE2=EF2+DF2﹣2EF×DFcos∠F=32+82﹣2×3×8×cos60°=49,
故答案为:6![]() ,49;
,49;
(2)证明:方法1,∵∠ACB=60°,
∴AB2=AC2+BC2﹣2ACBCcos60°=AC2+BC2﹣ACBC,
两边同时乘以![]() sin60°得,
sin60°得,![]() AB2sin60°=
AB2sin60°=![]() AC2sin60°+
AC2sin60°+![]() BC2sin60°﹣
BC2sin60°﹣![]() ACBCsin60°,
ACBCsin60°,
∵△ABC',△BCA',△ACB'是等边三角形,
∴S1=![]() ACBCsin60°,S2=
ACBCsin60°,S2=![]() AB2sin60°,S3=
AB2sin60°,S3=![]() BC2sin60°,S4=
BC2sin60°,S4=![]() AC2sin60°,
AC2sin60°,
∴S2=S4+S3﹣S1,∴S1+S2=S3+S4,
方法2、令∠A,∠B,∠C的对边分别为a,b,c,
∴S1=![]() absin∠C=
absin∠C=![]() absin60°=
absin60°=![]() ab
ab
∵△ABC',△BCA',△ACB'是等边三角形,
∴S2=![]() ccsin60°=
ccsin60°=![]() c2,S3=
c2,S3=![]() aasin60°=
aasin60°=![]() a2,S4=
a2,S4=![]() bbsin60°=
bbsin60°=![]() b2,
b2,
∴S1+S2=![]() (ab+c2),S3+S4=
(ab+c2),S3+S4=![]() (a2+b2),
(a2+b2),
∵c2=a2+b2﹣2abcos∠C=a2+b2﹣2abcos60°,
∴a2+b2=c2+ab,∴S1+S2=S3+S4.

 阅读快车系列答案
阅读快车系列答案