Question

【题目】如图，将边长为4的菱形纸片折叠，使点恰好落在对角线的交点处，若折痕，则（ ）

A． B． C． D．

Answer 1

【答案】A.

【解析】

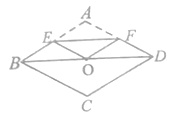
试题分析：连接AC，根据菱形的性质得出AC⊥BD，根据折叠得出EF⊥AC，EF平分AO，得出EF∥BD，得出EF为△ABD的中位线，根据三角形中位线定理求出BD的长，进而可得到BO的长，由勾股定理可求出AO的长，则∠ABO可求出，继而∠BAO的度数也可求出，再由菱形的性质可得∠A=2∠BAO．

连接AC，

∵四边形ABCD是菱形，∴AC⊥BD，

∵A沿EF折叠与O重合，∴EF⊥AC，EF平分AO，

∵AC⊥BD，∴EF∥BD，∴E、F分别为AB、AD的中点，

∴EF为△ABD的中位线，∴EF=BD，∴BD=2EF=4，

∴BO=2，∴AO==2，∴AO=AB，

∴∠ABO=30°，∴∠BAO=60°，∴∠BAD=120°．

故选A．