Question

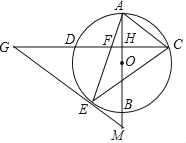
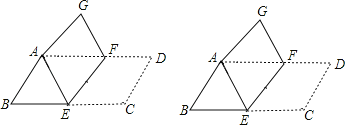
【题目】如图，将平行四边形ABCD纸片沿EF折叠，使点C与点A重合，点D落在点G处．

(1)连接CF，求证：四边形AECF是菱形；

(2)若E为BC中点，BC＝26，tan∠B＝，求EF的长．

Answer 1

【答案】(1)证明见解析；(2)EF＝10．

【解析】

(1)如图1，利用折叠性质得EA＝EC，∠1＝∠2，再证明∠1＝∠3得到AE＝AF，则可判断四边形AECF为平行四边形，从而得到四边形AECF为菱形；

(2)作EH⊥AB于H，如图，利用四边形AECF为菱形得到AE＝AF＝CE＝13，则判断四边形ABEF为平行四边形得到EF＝AB，根据等腰三角形的性质得AH＝BH，再在Rt△BEH中利用tanB＝＝可计算出BH＝5，从而得到EF＝AB＝2BH＝10．

(1)证明：如图1，

∵平行四边形ABCD纸片沿EF折叠，使点C与点A重合，点D落在点G处，

∴EA＝EC，∠1＝∠2，

∵四边形ABCD为平行四边形，

∴AD∥BC，

∴∠2＝∠3，

∴∠1＝∠3，

∴AE＝AF，

∴AF＝CE，

而AF∥CE，

∴四边形AECF为平行四边形，

∵EA＝EC，

∴四边形AECF为菱形；

(2)解：作EH⊥AB于H，如图，

∵E为BC中点，BC＝26，

∴BE＝EC＝13，

∵四边形AECF为菱形，

∴AE＝AF＝CE＝13，

∴AF＝BE，

∴四边形ABEF为平行四边形，

∴EF＝AB，

∵EA＝EB，EH⊥AB，

∴AH＝BH，

在Rt△BEH中，tanB＝＝，

设EH＝12x，BH＝5x，则BE＝13x，

∴13x＝13，解得x＝1，

∴BH＝5，

∴AB＝2BH＝10，

∴EF＝10．