题目内容
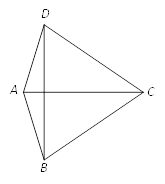
【题目】如图,在四边形ABCD中,AB=AD,AC是∠BAD的角平分线.
(1)求证:△ABC≌△ADC.
(2)若∠BCD=60°,AC=BC,求∠ADB的度数.
【答案】(1)详见解析;(2)∠ADB=15°.
【解析】
(1)根据角平分线的性质可得∠DAC=∠BAC,从而利用SAS,可判定全等.
(2)根据△ABC≌△ADC.可知BC=DC,∠ACB=∠ACD=30°,已知∠BCD=60°,故△BCD是等边三角形.即∠CBD=60°,在△ABC中AC=BC,∠ACB=30°,可得∠CDA=75°,进而求得∠ADB=15°.
解(1)∵AC是∠BAD的角平分线.
∴∠BAC=∠DAC,
∵AB=AD,AC=AC,
∴△ABC≌△ADC.
(2)∵△ABC≌△ADC.
∴BC=DC,∠ACB=∠ACD=30°,
∵∠BCD=60°,
∴△BCD是等边三角形.
∴∠CBD=60°,
∵AC=BC,
∴∠CDA=75°,
∴∠ADB=15°.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目