题目内容
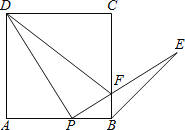
【题目】 如图,矩形ABCD中,过对角线BD中点O的直线分别交AB,CD边于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)只需添加一个条件,即______,可使四边形BEDF为菱形.

【答案】(1)详见解析;(2)EF⊥BD或DE=BE(答案不唯一)
【解析】
(1)根据平行四边形ABCD的性质,判定△BOE≌△DOF(ASA),得出四边形BEDF的对角线互相平分,进而得出结论;
(2)根据根据菱形的判定作出判断:对角线互相垂直的平行四边形是菱形或邻边相等的平行四边形是菱形.
(1)证明:∵四边形ABCD是平行四边形,O是BD的中点,
∴AB∥DC,OB=OD,
∴∠OBE=∠ODF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形;
(2)EF⊥BD或DE=BE(答案不唯一)
若添加EF⊥BD,由对角线互相垂直的平行四边形是菱形,所以平行四边形BEDF为菱形;
若添加DE=BE,由邻边相等的平行四边形是菱形,所以平行四边形BEDF为菱形;

练习册系列答案
相关题目