Question

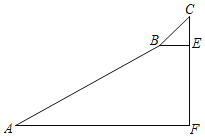
【题目】如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每段山坡近似是“直”的，测得坡长AB＝800米，BC＝200米，坡角∠BAF＝30°，坡角∠CBE＝45°，则山峰的高度为（　　）米．

A.500B.400+100C.D.541

Answer 1

【答案】B

【解析】

作BH⊥AF于H,在Rt△ABH中根据正弦的定义可计算出BH的长,从而得到EF的长；在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可求出山峰的高度．

解:作BH⊥AF于H,如图,

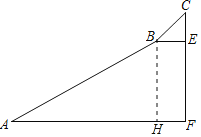
在Rt△ABH中,

∵sin∠BAH＝,

∴BH＝800sin30°＝400,

∴EF＝BH＝400米,

在Rt△CBE中,

∵sin∠CBE＝,

∴CE＝200sin45°＝100,

∴CF＝CE+EF＝（100+400）（米）．

答:山峰的高度CF为（100+400）米.

故选B．