Question

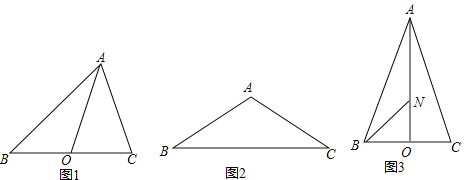
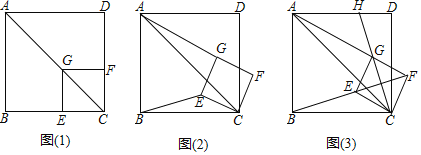
【题目】如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，GF⊥CD．

（1）①求证：四边形CEGF是正方形；②推断：的值为　　：

（2）将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系；

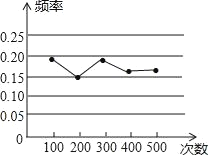
（3）正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG＝6，GH＝2，求正方形CEGF和正方形ABCD的边长．

Answer 1

【答案】（1）；（2）AG＝BE；（3）正方形CEGF的边长为3，正方形ABCD的边长为3．

【解析】

（1）①由GE⊥BC、GF⊥CD结合得∠BCD＝90°，可得四边形CEGF是矩形，再由∠ECG＝45°即可得证；

②由正方形性质知∠CEG＝∠B＝90°、∠ECG＝45°，据此可得＝、GE∥AB，利用平行线分线段成比例定理可得；

（2）连接CG，只需证△ACG∽△BCE即可得；

（3）证△AHG∽△CHA得＝，设BC＝CD＝AD＝a，知AC＝a，则由，得，计算AH＝，代入可得：a＝3，可得结论．

解：（1）①如图（1），∵四边形ABCD是正方形，

∴∠BCD＝90°，∠BCA＝45°，

∵GE⊥BC、GF⊥CD，

∴∠CEG＝∠CFG＝∠ECF＝90°，

∴四边形CEGF是矩形，∠CGE＝∠ECG＝45°，

∴EG＝EC，

∴四边形CEGF是正方形；

②由①知四边形CEGF是正方形，

∴∠CEG＝∠B＝90°，∠ECG＝45°，

∴＝，GE∥AB，

∴＝，

故答案为：；

（2）连接CG，

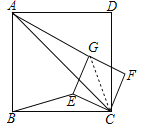
由旋转性质知∠BCE＝∠ACG＝α，

在Rt△CEG和Rt△CBA中，＝cos45°＝，＝cos45°＝，

∴＝，

∴△ACG∽△BCE，

∴＝，

∴线段AG与BE之间的数量关系为AG＝BE；

（3）∵∠CEF＝45°，点B、E、F三点共线，

∴∠BEC＝135°，

∵△ACG∽△BCE，

∴∠AGC＝∠BEC＝135°，

∴∠AGH＝∠CAH＝45°，

∵∠CHA＝∠AHG，

∴△AHG∽△CHA，

∴＝，

设BC＝CD＝AD＝a，则AC＝a，

则由，得

∴AH＝，

则DH＝AD﹣AH＝a，CH＝＝＝，

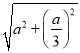∴得＝，

解得：a＝3，即BC＝3，CH＝×＝5，

∴CG＝CH﹣GH＝5﹣2＝3，

∵四边形CEGF是正方形，

∴CF＝3，

综上，正方形CEGF的边长为3，正方形ABCD的边长为3．