题目内容
(本题满分11分)
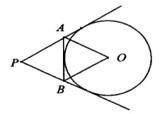
如图所示,⊙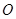 的直径
的直径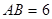 ,
,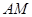 和
和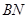 是它的两条切线,
是它的两条切线,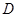 为射线
为射线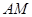 上的动点(不与
上的动点(不与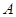 重合),
重合),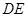 切⊙
切⊙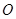 于
于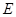 ,交
,交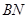 于
于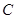 ,设
,设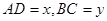 .
.
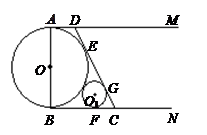
(1)求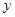 与
与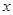 的函数关系式;
的函数关系式;
(2)若⊙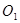 与⊙
与⊙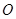 外切,且⊙
外切,且⊙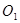 分别与
分别与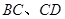
相切于点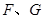 ,求
,求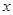 为何值时⊙
为何值时⊙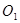 半径为1.
半径为1.
如图所示,⊙
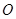 的直径
的直径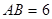 ,
,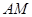 和
和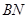 是它的两条切线,
是它的两条切线,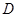 为射线
为射线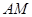 上的动点(不与
上的动点(不与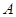 重合),
重合),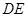 切⊙
切⊙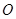 于
于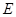 ,交
,交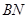 于
于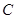 ,设
,设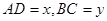 .
.
(1)求
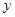 与
与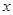 的函数关系式;
的函数关系式;(2)若⊙
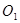 与⊙
与⊙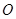 外切,且⊙
外切,且⊙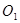 分别与
分别与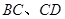
相切于点
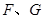 ,求
,求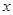 为何值时⊙
为何值时⊙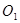 半径为1.
半径为1.解:(1)如图所示,作
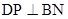 ,垂足为
,垂足为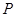 ……………1分
……………1分  ∵
∵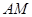 和
和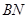 是⊙
是⊙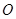 的两条切线
的两条切线∴
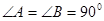
∴四边形
 为矩形
为矩形∴

∴
 ……………2分
……………2分 ∵
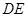 切⊙
切⊙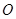 于
于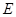
∴

∴
 ……………3分
……………3分 由
 ,得
,得 ……………4分
……………4分 即
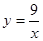 (
( )……………5分
)……………5分 (2)连接
 则
则 平分
平分 ,……………6分
,……………6分 ∵⊙
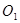 分别与
分别与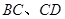 相切,
相切,∴
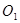 在
在 的角平分线
的角平分线 上,连接
上,连接 ,则
,则 ,作
,作 ,垂足为
,垂足为 ,则四边形
,则四边形 为矩形 ……………7分
为矩形 ……………7分 当⊙
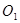 半径为1时,
半径为1时,
 , ……………8分
, ……………8分 ∴
 ,
, ……………9分
……………9分 ∴
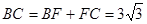 ……………10分
……………10分 ∴
 ,即当
,即当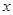 为
为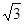 时,⊙
时,⊙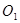 半径为1. ……………11分
半径为1. ……………11分 本题是关于圆的综合题,有一定难度。

练习册系列答案
相关题目
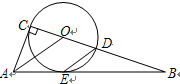
 交x轴于A、B两点,顶点为C,经过A、B、C三点的圆的圆心为M.
交x轴于A、B两点,顶点为C,经过A、B、C三点的圆的圆心为M.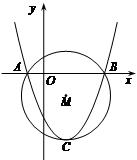 点D的坐标,若不存在,请说明理由.
点D的坐标,若不存在,请说明理由. 是
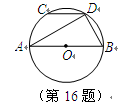
是 的直径,弦
的直径,弦
 .若
.若 ,则
,则 .
.
 是
是 的直径,弦
的直径,弦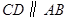 .若
.若 ,则
,则 .
.
 表示)
表示)