题目内容
(本小题满分8分)如图,抛物线 交x轴于A、B两点,顶点为C,经过A、B、C三点的圆的圆心为M.
交x轴于A、B两点,顶点为C,经过A、B、C三点的圆的圆心为M.
⑴ 求圆心M的坐标;
⑵ 求⊙M上劣弧AB的长;
⑶ 在抛物线上是否存在一点D,使线段OC和MD互相平分?若存在,直接写出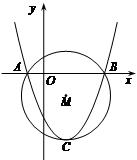 点D的坐标,若不存在,请说明理由.
点D的坐标,若不存在,请说明理由.
 交x轴于A、B两点,顶点为C,经过A、B、C三点的圆的圆心为M.
交x轴于A、B两点,顶点为C,经过A、B、C三点的圆的圆心为M.⑴ 求圆心M的坐标;
⑵ 求⊙M上劣弧AB的长;
⑶ 在抛物线上是否存在一点D,使线段OC和MD互相平分?若存在,直接写出
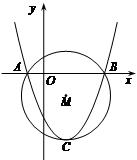 点D的坐标,若不存在,请说明理由.
点D的坐标,若不存在,请说明理由.解:⑴3分 ,∵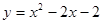 ∴
∴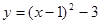
∴对称轴为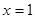 ,顶点
,顶点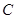 (1,-3)
(1,-3)
又∵抛物线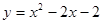 与
与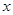 轴交点
轴交点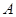 (
(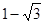 ,0)、
,0)、 (
(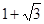 ,0)
,0)
∴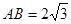
作抛物线对称轴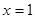 交
交 于点
于点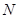 ,则
,则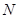 (1,0)
(1,0)
∴圆心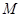 在对称轴
在对称轴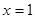 上,连接
上,连接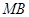
∵⊙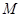 中,
中,
∴
设⊙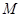 半径为
半径为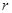 ,则
,则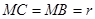
∵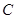 (1,-3)
(1,-3)
∴
∴
∵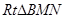 中
中
∴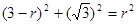 解得
解得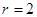
∴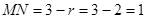
∵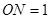
∴圆心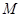 的坐标为(1,-1)
的坐标为(1,-1)
⑵3分,∵△BMN中,∠MNB=90°,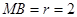 ,
,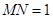
∴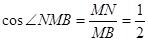
∴∠NMB=60°
∴∠AMB=2∠NMB=120°
∴⊙M上劣弧AB的长为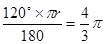
⑵ 2分,若线段OC和MD互相平分,则四边形 必定是平行四边形
必定是平行四边形
∴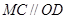 且
且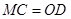
∵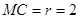
∴点 即为点
即为点 向下平移2个单位得点
向下平移2个单位得点
∴点 坐标为(0,-2)
坐标为(0,-2)
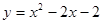 ∴
∴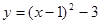
∴对称轴为
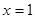 ,顶点
,顶点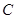 (1,-3)
(1,-3)又∵抛物线
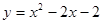 与
与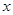 轴交点
轴交点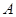 (
(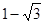 ,0)、
,0)、 (
(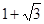 ,0)
,0)∴
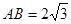
作抛物线对称轴
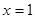 交
交 于点
于点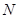 ,则
,则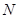 (1,0)
(1,0)∴圆心
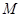 在对称轴
在对称轴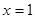 上,连接
上,连接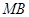
∵⊙
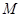 中,
中,
∴

设⊙
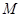 半径为
半径为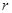 ,则
,则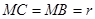
∵
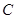 (1,-3)
(1,-3)∴

∴

∵
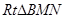 中
中
∴
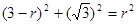 解得
解得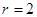
∴
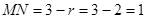
∵
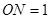
∴圆心
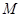 的坐标为(1,-1)
的坐标为(1,-1)⑵3分,∵△BMN中,∠MNB=90°,
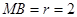 ,
,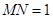
∴
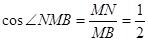
∴∠NMB=60°
∴∠AMB=2∠NMB=120°
∴⊙M上劣弧AB的长为
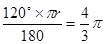
⑵ 2分,若线段OC和MD互相平分,则四边形
 必定是平行四边形
必定是平行四边形∴
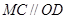 且
且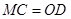
∵
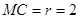
∴点
 即为点
即为点 向下平移2个单位得点
向下平移2个单位得点∴点
 坐标为(0,-2)
坐标为(0,-2)这是一道关于圆与二次函数的综合题,有一定的难度,需要学生对所学知识综合利用。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
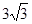 ,则圆锥的侧面积是 ▲ .
,则圆锥的侧面积是 ▲ .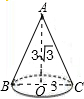
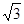 ,该平面上另有一点P,⊙P的半径为
,该平面上另有一点P,⊙P的半径为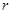 .请讨论⊙O与⊙P的位置关系.
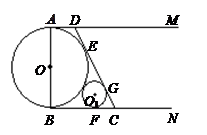
.请讨论⊙O与⊙P的位置关系.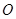 的直径
的直径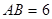 ,
,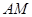 和
和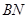 是它的两条切线,
是它的两条切线,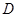 为射线
为射线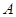 重合),
重合),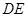 切⊙
切⊙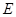 ,交
,交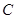 ,设
,设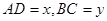 .
.
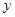 与
与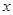 的函数关系式;
的函数关系式;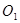 与⊙
与⊙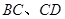
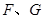 ,求
,求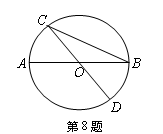

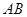 是
是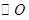 的直径,
的直径,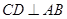 于E,连接AD、OC.
于E,连接AD、OC.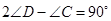 ;
;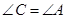 ,求∠D的度数.
,求∠D的度数.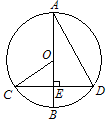
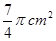 ,OC=3cm,求OA的长.
,OC=3cm,求OA的长.