题目内容
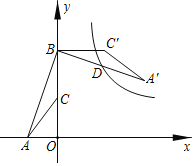
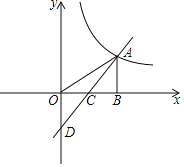
【题目】如图,直线AD与x轴交于点C,与双曲线y=![]() 交于点A,AB⊥x轴于点B(4,0),点D的坐标为(0,﹣2).
交于点A,AB⊥x轴于点B(4,0),点D的坐标为(0,﹣2).
(1)求直线AD的解析式;
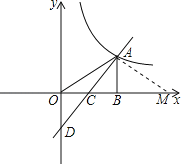
(2)若x轴上存在点M(不与点C重合),使得△AOC和△AOM相似,求点M的坐标.
【答案】(1)y=x﹣2;(2)(10,0)
【解析】
(1)先利用反比例函数解析式求出点A的坐标,设直线AD的解析式为y=kx+b,转化为方程组求出k,b即可解决问题.
(2)由题意点M只能在x轴的正半轴上,设OM=m,利用相似三角形的性质构建方程解决问题即可.
解:(1)把x=4代入![]() 得到y=2,
得到y=2,
∴A(4,2),
设直线AD的解析式为y=kx+b,
则有![]() ,
,
解得![]() .
.
∴直线AD的解析式为y=x﹣2.
(2)对于直线y=x﹣2,令y=0,得到x=2,
∴C(2,0),
∴OC=2,
∵A(4,2),
∴OA![]() ,
,
在△AOC中,∠ACO是钝角,
若M在x轴的负半轴上时,∠AOM>∠ACO,
因此两三角形不可能相似,所以点M只能在x轴的正半轴上,设OM=m,
∵M与C不重合,
∴△AOC∽△AOM不合题意舍弃,
∴当![]() ,即
,即![]() 时,△AOC∽△MOA,
时,△AOC∽△MOA,
解得m=10,
∴点M的坐标为(10,0).

【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
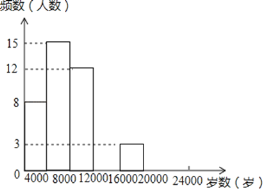
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37600名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,求被选取的两名教师恰好不在同一组的概率.