��Ŀ����
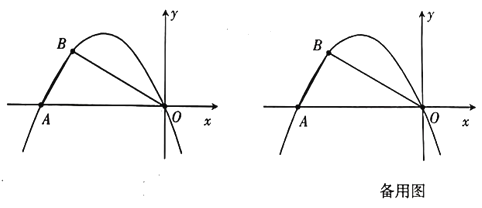
����Ŀ���ֽ������˶�����Խ��Խ����˹�ע��ϲ����ij��ȤС���������������50����ʦij�������˶����еIJ����������ͳ�����������������µ�ͳ��ͼ��������������
���� | Ƶ�� | Ƶ�� |
0��x��4000 | 8 | a |
4000��x��8000 | 15 | 0.3 |
8000��x��12000 | 12 | b |
12000��x��16000 | c | 0.2 |
16000��x��20000 | 3 | 0.06 |
20000��x��24000 | d | 0.04 |
�����������Ϣ������������⣺
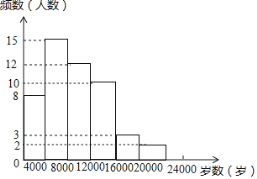
��1��д��a��b��c��d��ֵ����ȫƵ���ֲ�ֱ��ͼ��
��2������Լ��37600����ʦ���õ�����������ݹ��������߲�������12000��������12000�����Ľ�ʦ�ж�������
��3������50��������Ľ�ʦ�У�ѡȡ�����߲�������16000��������16000������������ʦ���ҷ����ĵã���ѡȡ��������ʦǡ�ò���ͬһ��ĸ��ʣ�
���𰸡���1��![]() ����ȫƵ���ֲ�ֱ��ͼ����������2�����������߲�������12000��������12000�����Ľ�ʦ��11280������3��
����ȫƵ���ֲ�ֱ��ͼ����������2�����������߲�������12000��������12000�����Ľ�ʦ��11280������3��![]()
��������
��1����8����50����a��ֵ����12����50����b��ֵ����50����0.2����c��ֵ����50����0.04����d��ֵ�������ɲ�ȫƵ���ֲ�ֱ��ͼ��
��2����37600���Ժ�3�����Ƶ��֮�ͼ��ý����
��3���������߲�����16000��x��20000��3����ʦ�ֱ�ΪA��B��C�������߲�����20000��x��24000��2����ʦ�ֱ�ΪX��Y���Ȼ�����״ͼ��ʾ�����еȿ��ܵ�����������ҳ�����������������Ȼ����ݸ��ʹ�ʽ���㼴�ɣ�
�⣺��1��a=8��50=0.16��b=12��50=0.24��c=50��0.2=10��d=50��0.04=2��
��ȫƵ���ֲ�ֱ��ͼ���£�
��2��37600����0.2+0.06+0.04��=11280��
�𣺹��������߲�������12000��������12000�����Ľ�ʦ��11280����
��3���������߲�����16000��x��20000��3����ʦ�ֱ�ΪA��B��C��
�����߲�����20000��x��24000��2����ʦ�ֱ�ΪX��Y��
����״ͼ���£�
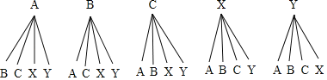
����״ͼ��֪������20�ֵȿ��ܵ���������б�ѡȡ��������ʦǡ�ò���ͬһ��Ĺ���12�������
����ѡȡ��������ʦǡ�ò���ͬһ��ĸ���=![]() ��
��

 ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д� �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�