题目内容
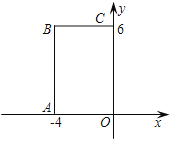
【题目】如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形
与矩形OABC关于点O位似，且矩形的面积等于矩形OABC面积的
，那么点
的坐标是_____．
【答案】（﹣2，3）或（2，﹣3）
【解析】
根据位似图形的概念得到矩形OA'B'C'∽矩形OABC，根据相似多边形的性质求出相似比，根据位似图形与坐标的关系计算，得到答案．
解：∵矩形OA'B'C'与矩形OABC关于点O位似，
∴矩形OA'B'C'∽矩形OABC，
∵矩形OA'B'C'的面积等于矩形OABC面积的
，
∴矩形OA'B'C'与矩形OABC的相似比为
，
∵点B的坐标为（﹣4，6），
∴点B'的坐标为（﹣4×，6×）或（4×，﹣6×），即（﹣2，3）或（2，﹣3），
故答案为：（﹣2，3）或（2，﹣3）．
练习册系列答案
相关题目
