Question

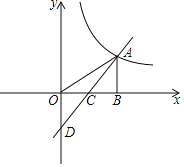
【题目】如图，点A的坐标是(﹣1，0)，点B的坐标是(0，6)，C为OB的中点，将△ABC绕点B逆时针旋转90°后得到△A'BC．若反比例函数y＝的图象恰好经过A'B的中点D，则k的值是（ ）

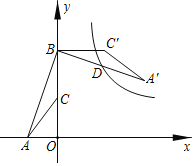
A.19B.16.5C.14D.11.5

Answer 1

【答案】B

【解析】

作A′H⊥y轴于H．证明△AOB≌△BHA′（AAS），推出OA＝BH，OB＝A′H，求出点A′坐标，再利用中点坐标公式求出点D坐标即可解决问题．

解：作A′H⊥y轴于H．

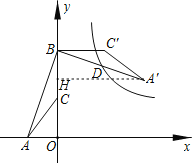
∵∠AOB＝∠A′HB＝∠ABA′＝90°，

∴∠ABO+∠A′BH＝90°，∠ABO+∠BAO＝90°，

∴∠BAO＝∠A′BH，

∵BA＝BA′，

∴△AOB≌△BHA′（AAS），

∴OA＝BH，OB＝A′H，

∵点A的坐标是（﹣1，0），点B的坐标是（0，6），

∴OA＝1，OB＝6，

∴BH＝OA＝1，A′H＝OB＝6，

∴OH＝5，

∴A′（6，5），

∵BD＝A′D，

∴D（3，5.5），

∵反比例函数y＝的图象经过点D，

∴k＝16.5．

故答案选：B．