题目内容
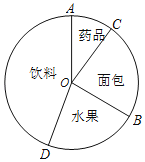
【题目】某商店购进
、
两种商品，购买1个商品比购买1个商品多花10元，并且花费300元购买商品和花费100元购买商品的数量相等．
（1）求购买一个商品和一个商品各需要多少元；
（2）商店准备购买、两种商品共80个，若商品的数量不少于商品数量的4倍，并且购买、商品的总费用不低于1000元且不高于1050元，那么商店有哪几种购买方案？
【答案】（1）购买一个
商品需要15元，购买一个
商品需要5元；（2）商店有2种购买方案，方案①：购进商品65个、商品15个；方案②：购进商品64个、商品16个．
【解析】
（1）设购买一个商品需要
元，则购买一个商品需要
元，根据数量＝总价÷单价结合花费300元购买商品和花费100元购买商品的数量相等，即可得出关于的分式方程，解之经检验后即可得出结论；
（2）设购买商品
个，则购买商品
个，根据商品的数量不少于商品数量的4倍并且购买、商品的总费用不低于1000元且不高于1050元，即可得出关于的一元一次不等式组，解之即可得出的取值范围，再结合为整数即可找出各购买方案．
解：（1）设购买一个商品需要元，则购买一个商品需要元，
依题意，得：
，
解得：
，
经检验，是原方程的解，且符合题意，
∴
．
答：购买一个商品需要15元，购买一个商品需要5元．
（2） 设购买商品个，则购买商品个，
依题意，得：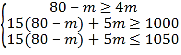
，
解得：
．
∵为整数，
∴
或16．
∴商店有2种购买方案，方案①：购进商品65个、商品15个；方案②：购进商品64个、商品16个．
【题目】某中学举办“网络安全知识答题竞赛”，七、八年级根据初赛成绩各选出5名选手组成代表队参加决赛，两个队各选出的5名选手的决赛成绩如图所示．
平均分（分） | 中位数（分） | 众数（分） | 方差（分2） | |
七年级 | a | 85 | b | S七年级2 |
八年级 | 85 | c | 100 | 160 |
（1）根据图示填空：a＝ ，b＝ ，c＝ ；
（2）结合两队成绩的平均数和中位数进行分析，哪个代表队的决赛成绩较好？
（3）计算七年级代表队决赛成绩的方差S七年级2，并判断哪一个代表队选手成绩较为稳定．
