题目内容
如图,已知在Rt△ABC中,∠ACB=90°,BC>AC,⊙O为△ABC的外接圆,以点C为圆心,BC长为半径作弧交CA的延长线于点D,交⊙O于点E,连接BE、DE.
(l)求∠DEB的度数;
(2)若直线DE交⊙0于点F,判断点F在半圆AB上的位置,并证明你的结论.

(l)求∠DEB的度数;
(2)若直线DE交⊙0于点F,判断点F在半圆AB上的位置,并证明你的结论.

(1)连接CE、BD,
∵∠BDE与∠ECB所对的弧都为弧EB,
∴∠BDE=
∠ECB,
同理:∠DBE=
∠ECD,
∴∠BDE+∠DBE=
∠DCB,
∵∠ACB=90°,
∴∠BDE+∠DBE=45°,
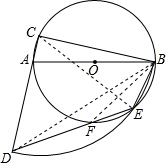 ∴∠DEB=180°-(∠BDE+∠DBE)=135°;
∴∠DEB=180°-(∠BDE+∠DBE)=135°;
(2)F为弧AB中点.
理由:连接BF,由(1)知∠DEB=135°,
∴∠CED=45°
∴∠ABF=45°,
∴
=
,
即F为弧AB中点.
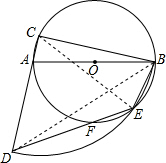
∵∠BDE与∠ECB所对的弧都为弧EB,
∴∠BDE=
| 1 |
| 2 |
同理:∠DBE=
| 1 |
| 2 |
∴∠BDE+∠DBE=
| 1 |
| 2 |
∵∠ACB=90°,
∴∠BDE+∠DBE=45°,
 ∴∠DEB=180°-(∠BDE+∠DBE)=135°;
∴∠DEB=180°-(∠BDE+∠DBE)=135°;(2)F为弧AB中点.
理由:连接BF,由(1)知∠DEB=135°,
∴∠CED=45°
∴∠ABF=45°,
∴
 |
| AF |
| 1 |
| 2 |
 |
| AB |
即F为弧AB中点.


练习册系列答案
相关题目







