题目内容
若圆的一条弦把圆分成度数之比为1：3的两条弧，则这条弦所对的圆周角等于（ ）
| A．45° | B．135° | C．90°和270 | D．45°和135° |
如图，弦AB将⊙O分成了度数比为1：3两条弧．
连接OA、OB；则∠AOB=90°；
①当所求的圆周角顶点位于D点时，
这条弦所对的圆周角∠ADB=
∠AOB=45°；
②当所求的圆周角顶点位于C点时，
这条弦所对的圆周角∠ACB=180°-∠ADB=135°．
故选D．
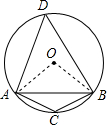
连接OA、OB；则∠AOB=90°；
①当所求的圆周角顶点位于D点时，
这条弦所对的圆周角∠ADB=
| 1 |
| 2 |
②当所求的圆周角顶点位于C点时，
这条弦所对的圆周角∠ACB=180°-∠ADB=135°．
故选D．
练习册系列答案
提分百分百检测卷系列答案
相关题目
