题目内容
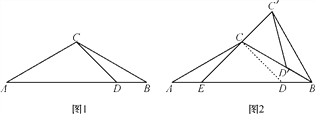
【题目】如图1,△ABC中,AC=BC,∠A=30°,点D在AB边上,且∠ADC=45°.
(1)求∠BCD的度数;
(2)将图1中的△BCD绕点B顺时针旋转得到△BC′D′,当点D′恰好落在BC边上时,如图2所示,连接C′C并延长交AB于点E.
①求∠C′CB的度数;
②求证:△C′BD′≌△CAE.
【答案】(1)15° (2)①75° ②见解析
【解析】【试题分析】
(1)AC=BC,∠A=30°,根据等边对等角得,∠B=∠A=30°.
因为∠ADC=45°,根据外角的性质得,∠BCD=∠ADC-∠B=15°.
(2)①由旋转的性质得,得BC=BC′=AC,∠C′BD′=∠CBD=∠A=30°.
在等腰三角形![]() 中,根据的内角和定理得,∠CC′B=∠C′CB=75°.
中,根据的内角和定理得,∠CC′B=∠C′CB=75°.
②在![]() 中,利用外角的性质得,∠CEB=∠C′CB-∠CBA=45°,
中,利用外角的性质得,∠CEB=∠C′CB-∠CBA=45°,
在![]() 中,∠ACE=∠CEB-∠A=15°.等量代换得,∠BC′D′=∠BCD=∠ACE.
中,∠ACE=∠CEB-∠A=15°.等量代换得,∠BC′D′=∠BCD=∠ACE.
在△C′BD′和△CAE中,
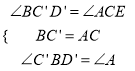
利用SAS判定得,△C′BD′≌△CAE.
【试题解析】
(1)∵AC=BC,∠A=30°,∴∠B=∠A=30°.
∵∠ADC=45°,∴∠BCD=∠ADC-∠B=15°.
(2)①由旋转,得BC=BC′=AC,∠C′BD′=∠CBD=∠A=30°.
∴∠CC′B=∠C′CB=75°.
②证明:∵∠CEB=∠C′CB-∠CBA=45°,
∴∠ACE=∠CEB-∠A=15°.
∴∠BC′D′=∠BCD=∠ACE.
在△C′BD′和△CAE中,
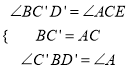
∴△C′BD′≌△CAE(ASA).

练习册系列答案
相关题目