题目内容
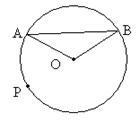
如图,在△ABD中,∠A=∠B=30°,以AB边上一点O为圆心,过A,D两点作⊙O交AB于C.
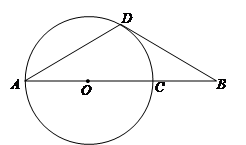
小题1:判断直线BD与⊙O的位置关系,并说明理由;
小题2:连接CD,若CD=5,求AB的长.

小题1:判断直线BD与⊙O的位置关系,并说明理由;
小题2:连接CD,若CD=5,求AB的长.
小题1:直线BD与⊙O相切.
理由如下:如图,连接OD,
∵∠ODA=∠DAB=∠B=30°,
∴∠ODB=180°-∠ODA-∠DAB-∠B=180°-30°-30°-30°=90°,
即OD⊥BD, ∴直线BD与⊙O相切.
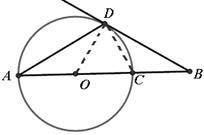
小题1:由(1)知,∠ODA=∠DAB=30°,
∴∠DOB=∠ODA+∠DAB=60°,
又∵OC=OD,
∴△DOC是等边三角形,
∴OA=OD=CD=5.
又∵∠B=30°,∠ODB=90°,
∴OB=2OD=10. ∴AB=OA+OB=5+10=15.
证出OD⊥BD,即可证明直线BD与⊙O相切。直角三角形中,30°角所对的直角边等于斜边的一半。

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
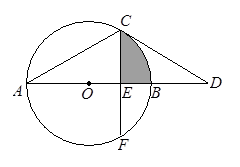
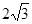 ,求图中阴影部分的面积.
,求图中阴影部分的面积.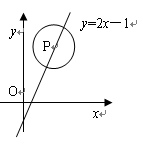
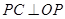 ,PC交⊙O于点C,若AP=4,PB=2,则PC的长为__◆ .
,PC交⊙O于点C,若AP=4,PB=2,则PC的长为__◆ .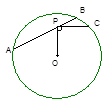
 . 动点O在AC上,以点O为圆心,OA长为半径的⊙O分别交AB、AC于点D、E,连结CD.
. 动点O在AC上,以点O为圆心,OA长为半径的⊙O分别交AB、AC于点D、E,连结CD.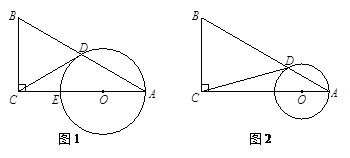
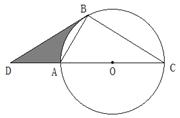
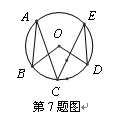
 ,⊙O上一动点P从A点出发,沿逆时针方向运动一周,当S
,⊙O上一动点P从A点出发,沿逆时针方向运动一周,当S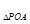 =S
=S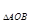 时,则点P所经过的弧长是
时,则点P所经过的弧长是